Yangcheng Li
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 4, Pages 825–831
DOI: 10.7546/nntdm.2024.30.4.825-831
Full paper (PDF, 223 Kb)
Details
Authors and affiliations
Yangcheng Li ![]()
School of Mathematical Sciences, South China Normal University
Guangzhou, People’s Republic of China
Abstract
We prove that, for ![]() , the Diophantine equation
, the Diophantine equation ![]() in positive integers
in positive integers ![]() with
with ![]() , has no solutions satisfying
, has no solutions satisfying ![]() or
or ![]() .
.
Keywords
- Diophantine equation
- Diophantine approximation
2020 Mathematics Subject Classification
- 11D41
- 11D61
References
- Bennett, M. A. (1997). Explicit lower bounds for rational approximation to algebraic numbers. Proceedings of the London Mathematical Society, 75, 63–78.
- Bennett, M. A. (2007). The Diophantine equation
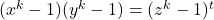 . Indagationes Mathematicae, 18, 507–525.
. Indagationes Mathematicae, 18, 507–525. - Bugeaud, Y. (2004). On the Diophantine equation
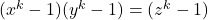 . Indagationes Mathematicae, 15, 21–28.
. Indagationes Mathematicae, 15, 21–28. - Bugeaud, Y., & Dujella, A. (2003). On a problem of Diophantus for higher powers. Mathematical Proceedings of the Cambridge Philosophical Society, 135(1), 1–10.
- Dickson, L. E. (1966). History of the Theory of Numbers, Vol. 2, pp. 513–520. Chelsea, New York.
- Goedhart, E. G., & Grundman, H. G. (2015). Diophantine approximation and the equation
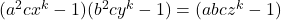 . Journal of Number Theory, 154, 74–81.
. Journal of Number Theory, 154, 74–81. - Guy, R. K. (2004). Unsolved Problems in Number Theory (3rd ed.). Springer, New York.
- Hai, Y., & Walsh, P. G. (2010). On a Diophantine problem of Bennett. Acta Arithmetica, 145(2), 129–136.
- Kashihara, K. (1990). The Diophantine equation
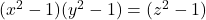 . Research Reports of the Anan College of Technology. 26, 119–130.
. Research Reports of the Anan College of Technology. 26, 119–130. - Maple software. https://cn.maplesoft.com/products/maple/.
- Zhang, Z. (2014). The Diophantine equation
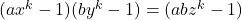 . Journal of Number Theory, 136, 252–260.
. Journal of Number Theory, 136, 252–260.
Manuscript history
- Received: 5 July 2023
- Revised: 7 November 2024
- Accepted: 24 November 2024
- Online First: 30 November 2024
Copyright information
![]() Ⓒ 2024 by the Author.
Ⓒ 2024 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Li, Y. (2024). A note on the Diophantine equation ![]() . Notes on Number Theory and Discrete Mathematics, 30(4), 811-824, DOI: 10.7546/nntdm.2024.30.4.825-831.
. Notes on Number Theory and Discrete Mathematics, 30(4), 811-824, DOI: 10.7546/nntdm.2024.30.4.825-831.


