Revisiting some r-Fibonacci sequences and Hessenberg matrices

Carlos M. da Fonseca, Paulo Saraiva and Anthony G. Shannon
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 4, Pages 704–715
DOI: 10.7546/nntdm.2024.30.4.704-715
Full paper (PDF, 244 Kb)

Details

Authors and affiliations

Carlos M. da Fonseca
¹ Kuwait College of Science and Technology
Doha District, Safat 13133, Kuwait
² Faculty of Applied Mathematics and Informatics, Technical University of Sofia
Kliment Ohridski Blvd. 8, 1000 Sofia, Bulgaria
³ Chair of Computational Mathematics, University of Deusto
48007 Bilbao, Spain

Paulo Saraiva
⁴ Faculty of Economics, University of Coimbra
Av. Dias da Silva, 165, 3004-512 Coimbra, Portugal
⁵ CMUC, Department of Mathematics, University of Coimbra
3000-143 Coimbra, Portugal
⁶ CeBER-Centre for Business and Economics Research
Av. Dias da Silva, 165, 3004-512 Coimbra, Portugal

Anthony G. Shannon
Honorary Fellow, Warrane College
University of New South Wales, NSW 2033, Australia

Abstract

The relationship between different generalizations of Fibonacci numbers and matrices is common in the literature. However, the basic relation of such sequences with Hessenberg matrices is often not properly explored. In this work we revisit some classic results and present some applications in recent contexts.

Keywords

• Hessenberg matrices
• r-Fibonacci sequence
• Recurrence relations
• Determinant
• Matrices

2020 Mathematics Subject Classification

• 15A15
• 11B39

References

1. Abbad, S., Belhachir, H., & Benali, B. (2019). Companion sequences associated to the r-Fibonacci sequence: Algebraic and combinatorial properties. Turkish Journal of Mathematics, 43, 1095–1114.
2. Anđelic, M., Du, Z., da Fonseca, C. M., & Kılıç, E. (2020). A matrix approach to some second-order difference equations with sign-alternating coefficients. Journal of Difference Equations and Applications, 26, 149–162.
3. Anđelic, M., da Fonseca, C. M., & Yılmaz, F. (2022). The bi-periodic Horadam sequence and some perturbed tridiagonal 2-Toeplitz matrices: A unified approach. Heliyon, 8, Article E08863.
4. Austin, R., & Guy, R. (1978). Binary sequences without isolated ones. The Fibonacci Quarterly, 16, 84–87.
5. Bednarz, U., & Wołowiec-Musiał, M. (2020). Distance Fibonacci polynomials. Symmetry, 12, Article 1540.
6. Belbachir, H., & Djellas, I.E. (2022). Determinantal and permanental representations of companion sequences associated to the r-Fibonacci sequence. Notes on Number Theory and Discrete Mathematics, 28(1), 64–74.
7. Bród, D. (2015). On distance (r, k)-Fibonacci numbers and their combinatorial and graph interpretations. Journal of Applied Mathematics, 2015, Article ID 879510.
8. Deveci, Ö., & Shannon, A. G. (2023). A study on recurrence relations for binary sequence matrices. Advanced Studies in Contemporary Mathematics, 33, 17–21.
9. Deveci, Ö., & Shannon, A. G. (2021). The complex-type k-Fibonacci sequences and their applications. Communications in Algebra, 49, 1352–1367.
10. Flores, I. (1967). Direct calculation of k-generalized Fibonacci numbers. The Fibonacci Quarterly, 5, 259–266.
11. da Fonseca, C. M. (2011). An identity between the determinant and the permanent of Hessenberg-type matrices. Czechoslovak Mathematical Journal, 61(136), 917–921.
12. Getu, S. (1991). Evaluating determinants via generating functions. Mathematics Magazine, 64, 45–53.
13. Hoffman, H. F. (2014). Innovative Capstone Project Examples. In Harvey F. Hoffman, The Engineering Capstone Course: Fundamentals for Students and Instructors. Cham, Sui: Springer, 99–112.
14. Inselberg, A. (1978). On determinants of Toeplitz–Hessenberg matrices arising in power series. Journal of Mathematical Analysis and Applications, 63, 347–353.
15. Iverson, K. E. (1980). Notation as a tool of thought. Communications of the Association for Computing Machinery, 23, 444–465.
16. Jancic, M. (2012). Determinants and recurrence sequences. Journal of Integer Sequences, 15, Article 12.3.5.
17. Kuloglu, B., & Özkan, E. (2022). On generalized (k, r)-Pell and (k, r)-Pell–Lucas numbers. Notes on Number Theory and Discrete Mathematics, 28(4), 765–777.
18. Melham, R. S., & Shannon, A. G. (1995). Some summation identities using generalized Q-matrices. The Fibonacci Quarterly, 33, 64–73.
19. Merca, M. (2013). A note on the determinant of a Toeplitz–Hessenberg matrix. Special Matrices, 1, 10–16.
20. Miles Jr., E.P. (1960). Generalized Fibonacci numbers and associated matrices. The American Mathematical Monthly, 67, 745–752.
21. Muir, T. (1960). The Theory of Determinants in the Historical Order of Development, Vol. IV, Dover Publications, New York.
22. Noe, T. D., & Post, J. V. (2005). Primes in Fibonacci n-step and Lucas n-step sequences. Journal of Integer Sequences, 8, Article 05.4.4.
23. Shannon, A. G. (2009). Generalized Fibonacci matrices in medicine. Notes on Number Theory and Discrete Mathematics, 15, 12–21.
24. Shannon, A. G., & Ollerton, R. L. (2002). Combinatorial matrices and linear recursive sequences. The Fibonacci Quarterly, 40, 417–423.
25. Tuğlu, N., Koçer, E. G., & Stakhov, A. (2011). Bivariate Fibonacci like p-polynomials. Applied Mathematics and Computation, 217, 10239–10246.
26. Udrea, G. (1996). A note on the sequence 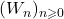of A. F. Horadam. Portugaliae Mathematica, 53, 143–155.
27. Vein, R., & Dale, P. (1999). Determinants and their Applications in Mathematical Physics. Applied Mathematical Sciences, 134. Springer, New York.
28. Verde-Star, L. (2017). Polynomial sequences generated by infinite Hessenberg matrices. Special Matrices, 5, 64–72.
29. Verde-Star, L. (2015). Elementary triangular matrices and inverses of k-Hessenberg matrices and triangular matrices. Special Matrices, 3, 250–256.

Manuscript history

• Received: 28 May 2024
• Revised: 29 October 2024
• Accepted: 1 November 2024
• Online First: 8 November 2024

Copyright information

Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).