Pentti Haukkanen
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 4, Pages 681–690
DOI: 10.7546/nntdm.2024.30.4.681-690
Full paper (PDF, 221 Kb)
Details
Authors and affiliations
Pentti Haukkanen ![]()
![]()
Faculty of Information Technology and Communication Sciences,
FI-33014 Tampere University, Finland
Abstract
This paper gives expressions for the solution ![]() of the equation
of the equation
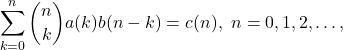
where ![]() , that is, of the equation
, that is, of the equation ![]() in
in ![]() , where
, where ![]() is the binomial convolution. These expressions are classified as recursive, explicit, determinant, exponential generating function and convolutional expressions. These expressions are compared with those under the usual Cauchy convolution. Several special cases and examples of combinatorial nature are also discussed.
is the binomial convolution. These expressions are classified as recursive, explicit, determinant, exponential generating function and convolutional expressions. These expressions are compared with those under the usual Cauchy convolution. Several special cases and examples of combinatorial nature are also discussed.
Keywords
- Arithmetical equation
- Binomial convolution
- Cauchy convolution
- Exponential generating function
- Binomial coefficient
2020 Mathematics Subject Classification
- 05A10
- 11A25
- 11B65
References
- Aigner, M. (1979). Combinatorial Theory. Springer-Verlag, New York.
- Alecci, G., Barbero, S., & Murru, N. (2023). Some notes on the algebraic structure of linear recurrent sequences. Ricerche di Matematica, 1–17.
- Batır, N., & Sofo, A. (2023). Sums involving the binomial coefficients, Bernoulli numbers of the second kind and harmonic numbers. Notes on Number Theory and Discrete Mathematics, 29(1), 78–97.
- Gessel, I. M., & Kar, I. (2024). Binomial convolutions for rational power series. Journal of Integer Sequences, 27(1), Article 24.1.3.
- Graham, R. L., Knuth, D. E., & Patashnik, O. (1989). Concrete Mathematics: A Foundation for Computer Science. Addison-Wesley Publishing Company, New York.
- Haukkanen, P. (1994). Roots of sequences under convolutions. The Fibonacci Quarterly, 32, 369–372.
- Haukkanen, P. (1996). On a binomial convolution of arithmetical functions. Nieuw Archief voor Wiskunde, 14, 209–216.
- Haukkanen, P. (2023). Quotients of arithmetical functions under the Dirichlet convolution. Notes on Number Theory and Discrete Mathematics, 29(2), 185–194.
- Kılıç, E., Akkuş, I., Ömür, N., & Ulutaş, Y. T. (2016). Generalized binomial convolution of the mth powers of the consecutive integers with the general Fibonacci sequence. Demonstratio Mathematica, 49(4), 379–385.
- Pellegrino, F. (1963). La divisione integrale. Rendiconti di Matematica e delle sue
Applicazioni, 22(5), 489–497. - Riordan, J. (1958). An Introduction to Combinatorial Analysis. John Wiley and Sons, New York.
- Schinzel, A. (1998). A property of the unitary convolution. Colloquium Mathematicae, 78(1), 93–96.
- Singh, J. (2014). On an arithmetic convolution. Journal of Integer Sequences, 17(2), Article 14.6.7.
- Srisopha, S., Ruengsinsub, P., & Pabhapote, N. (2012). The Qα–convolution of arithmetic functions and some of its properties. East–West Journal of Mathematics, 14(01), 76–83.
- Succi, F. (1956). Sulla espressione del quoziente integrale di due funzioni aritmetiche. Rendiconti di Matematica e delle sue Applicazioni, 15(5), 80–92.
Manuscript history
- Received: 15 August 2024
- Revised: 25 October 2024
- Accepted: 26 October 2024
- Online First: 5 November 2024
Copyright information
![]() Ⓒ 2024 by the Author.
Ⓒ 2024 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Batır, N., & Sofo, A. (2023). Sums involving the binomial coefficients, Bernoulli numbers of the second kind and harmonic numbers. Notes on Number Theory and Discrete Mathematics, 29(1), 78–97.
- Haukkanen, P. (2023). Quotients of arithmetical functions under the Dirichlet convolution. Notes on Number Theory and Discrete Mathematics, 29(2), 185–194.
Cite this paper
Haukkanen, P. (2024). Quotients of sequences under the binomial convolution. Notes on Number Theory and Discrete Mathematics, 30(4), 681-690, DOI: 10.7546/nntdm.2024.30.4.681-690.


