Carlos M. da Fonseca and Anthony G. Shannon
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 3, Pages 491–498
DOI: 10.7546/nntdm.2024.30.3.491-498
Full paper (PDF, 200 Kb)
Details
Authors and affiliations
Carlos M. da Fonseca ![]()
![]()
1 Kuwait College of Science and Technology
Doha District, Safat 13133, Kuwait
2 Chair of Computational Mathematics, University of Deusto
48007 Bilbao, Spain
Anthony G. Shannon ![]()
3 Honorary Fellow, Warrane College, University of New South Wales
2033, Australia
Abstract
In this note, old and new properties of Fermatian numbers ![]() are recalled. A new formal operator is defined and some identities and extensions are discussed.
are recalled. A new formal operator is defined and some identities and extensions are discussed.
Keywords
- Fermatian numbers
- Recurrence relation
- Formal operators
2020 Mathematics Subject Classification
- 11B39
- 11B75
- 11B65
- 05A30
References
- Anđelic, M., da Fonseca, C. M., & Yılmaz, F. (2022). The bi-periodic Horadam sequence and some perturbed tridiagonal 2-Toeplitz matrices: A unified approach. Heliyon, 8, Article E08863.
- Bondarenko, B. A. (1993). Generalized Pascal Triangles and Pyramids: Their Fractals, Graphs and Applications. Translated by R. C. Bollinger. Santa Clara, CA: The Fibonacci Association.
- Carlitz, L. (1940). A set of polynomials. Duke Mathematical Journal, 6, 486–504.
- Carlitz, L. (1948). q-Bernoulli numbers and polynomials. Duke Mathematical Journal, 15, 987–1000.
- Cox, N. J., & Hoggatt Jr., V. E. (1970). Some universal counter examples. The Fibonacci Quarterly, 8, 242–248.
- Guy, R. K. (1994). Unsolved Problems in Number Theory. (2nd ed.). New York, Springer-Verlag, pp. 28–29.
- Hoggatt Jr., V. E., & Bicknell, M. (1969). Diagonal sums of generalized Pascal triangles. The Fibonacci Quarterly, 7, 341–358.
- Jameson, G. J. O. (2011). Finding Carmichael numbers. Mathematical Gazette, 95, 244–255.
- Pinch, R. G. E. (2000). The pseudoprimes up to
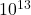 . Algorithmic Number Theory, Lecture Notes in Computer Science, Vol. 1838, 459–473. Springer, Leiden.
. Algorithmic Number Theory, Lecture Notes in Computer Science, Vol. 1838, 459–473. Springer, Leiden. - Pomerance, C., Selfridge, J. L., & Wagstaff Jr., S. S. (1980). The pseudoprimes to
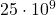 . Mathematics of Computation, 35, 1003–1026.
. Mathematics of Computation, 35, 1003–1026. - Sàndor, J., & Atanassov, K. T. (2021). Chapter 1. Arithmetic Functions. New York, Nova Science Publishers.
- Shanks, D. (1993). Solved and Unsolved Problems in Number Theory (4th ed.). New York, Chelsea, pp. 115-117.
- Shannon, A. G. (2003). Some Fermatian special functions. Notes on Number Theory and Discrete Mathematics, 9(4), 73–82.
- Shannon, A. G. (2004). Some properties of Fermatian numbers. Notes on Number Theory and Discrete Mathematics, 10(2), 25–33.
- Shannon, A. G. (2004). A Fermatian Staudt–Clausen Theorem. Notes on Number Theory and Discrete Mathematics, 10(4), 89–99.
- Shannon, A. G. (2010). Fermatian analogues of Gould’s generalized Bernoulli polynomials. Notes on Number Theory and Discrete Mathematics, 16(4), 14–17.
- Shannon, A. G. (2019). Applications of Mollie Horadam’s generalized integers to Fermatian and Fibonacci numbers. Notes on Number Theory and Discrete Mathematics, 25(2), 113–126.
- Sloane, N. J. A. (2024). The On-Line Encyclopedia of Integer Sequences. Available online at: http://oeis.org.
- Sylvester, J. J. (1912). Chapters 1, 4. The Collected Papers, Volume IV (1882–1897). Cambridge University Press.
- Udrea, G. (1996). A note on the sequence
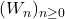 of A. F. Horadam. Portugaliae Mathematica, 53, 143–155.
of A. F. Horadam. Portugaliae Mathematica, 53, 143–155. - Vandiver, H. S. (1941). Simple explicit expressions for generalized Bernoulli numbers. Duke Mathematical Journal, 8, 575–584.
- Vorob’ev, N. N. (1980). Criteria for Divisibility. University of Chicago Press, Chapter 3.
- Ward, M. (1936). A calculus of sequences. American Journal of Mathematics, 58, 255–266.
- Weisstein, E. W. (2005). Poulet Number. MathWorld – A Wolfram Web Resource. Available online at: https://mathworld.wolfram.com/PouletNumber.html
Manuscript history
- Received: 9 April 2024
- Revised: 16 August 2024
- Accepted: 18 August 2024
- Online First: 26 September 2024
Copyright information
![]() Ⓒ 2024 by the Authors.
Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Shannon, A. G., Uysal, M., & Özkan, E. (2025). Fermatian row and column sums as a family of generalized integers. Notes on Number Theory and Discrete Mathematics, 31(3), 433-442.
- Shannon, A. G. (2019). Applications of Mollie Horadam’s generalized integers to Fermatian and Fibonacci numbers. Notes on Number Theory and Discrete Mathematics, 25(2), 113–126.
- Shannon, A. G. (2010). Fermatian analogues of Gould’s generalized Bernoulli polynomials. Notes on Number Theory and Discrete Mathematics, 16(4), 14–17.
- Shannon, A. G. (2004). A Fermatian Staudt–Clausen Theorem. Notes on Number Theory and Discrete Mathematics, 10(4), 89–99.
- Shannon, A. G. (2004). Some properties of Fermatian numbers. Notes on Number Theory and Discrete Mathematics, 10(2), 25–33.
- Shannon, A. G. (2003). Some Fermatian special functions. Notes on Number Theory and Discrete Mathematics, 9(4), 73–82.
Cite this paper
Da Fonseca, C. M., & Shannon, A. G. (2024). A formal operator involving Fermatian numbers. Notes on Number Theory and Discrete Mathematics, 30(3), 491-498, DOI: 10.7546/nntdm.2024.30.3.491-498.


