Some properties of Fermatian numbers

A. G. Shannon
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 10, 2004, Number 2, Pages 25–33
Full paper (PDF, 152 Kb)

Details

Authors and affiliations

A. G. Shannon
Warrane College, The University of New South Wales, Kensington 1465, &
KvB Institute of Technology, 99 Mount Street, North Sydney, NSW 2065, Australia

Abstract

This paper looks at some basic number theoretic properties of Fermatian numbers. We define the n-th reduced Fermatian number in terms of

\underline{q}_n = \begin{array}{l l} -q^n \underline{q}_{-n} & \quad (n < 0) \\ 1 & \quad (n = 1) \\ 1 + q + q^2 + ... + q^{n-1} & \quad (n > 0) \end{array} .

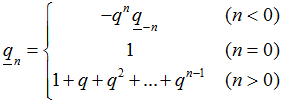
so that 1n = n, and 1n! = n!, where qn! = qnqn−1…q1.
Some congruence properties and relationships with Bernoulli and Fibonacci numbers are explored. Some aspects of the notation and meaning of the Fermatian numbers are also outlined.

AMS Classification

  • 11B65
  • 11B39
  • 05A30

References

  1. L. Carlitz. A Set of Polynomials. Duke Mathematical Journal. 6 (1940): 486-504.
  2. L. Carlitz. q-Bernoulli Numbers and Polynomials. Duke Mathematical Journal. 15 (1948): 987-1000.
  3. L. Carlitz. A Theorem of Glaisher. Canadian Journal of Mathematics. 5 (1953): 306-316.
  4. L. Carlitz. Note on a Theorem of Glaisher.  Journal of the London Mathematical Society. 28 (1953): 245-246.
  5. L. Carlitz. Extension of a Theorem of Glaisher and Some Related Results. Bulletin of the Calcutta Mathematical Society. 46 (1954): 77-80.
  6. L. Carlitz. A Note on the Generalized Wilson’s Theorem. American Mathematical Monthly. 71 (1964): 291-293.
  7. L. Carlitz. The Highest Power of a Prime Dividing Certain Quotients. Archiv der Mathematik. 18 (1967): 153-159.
  8. L. Carlitz. Some Identities in Combinatorial Analysis. Duke Mathematical Journal 38 (1971): 51-56.
  9. L. Carlitz & L. Moser. On Some Special Factorizations of . Canadian Mathematical Bulletin. 9 (1966): 421-426.
  10. A. L. Cauchy. Memoire sur les functions don’t plusiers valeurs. Comptes rendus de l’Académie des Sciences. 17 (1843): 526-534.
  11. N. Cox, J. W. Phillips & V.E. Hoggatt Jr. Some Universal Counterexamples. The Fibonacci Quarterly. (1970): 242-248.
  12. L. E. Dickson. History of the Theory of Numbers.Volume 1.  NewYork: Chelsea, 1952.
  13. M. Feinberg. Fibonacci-tribonacci.The Fibonacci Quarterly. 1(3) (1963): 71-74.
  14. M. Feinberg. New Slants. The Fibonacci Quarterly. 2(1964): 223-227.
  15. G. Fontené. Generalization d’une formule connue. Nouvelles Annales Mathématiques. 15 (1915): 112.
  16. H. W. Gould. The Bracket Function and Fontené-Ward Generalized Binomial Coefficients with Application to Fibonacci Coefficients. The Fibonacci Quarterly. 7 (1969): 23-40,55.
  17. G. H. Hardy & E. M. Wright. An Introduction to the Theory of Numbers. Oxford: The Clarendon Press, 1965.
  18. V. E. Hoggatt Jr & M. Bicknell. Diagonal Sums of Generalized Pascal Triangles. The Fibonacci Quarterly. 7 (1969): 341-358.
  19. A. F. Horadam. Generating Functions for Powers of a Certain Generalized Sequence of Numbers. Duke Mathematical Journal. 32 (1965): 437-446.
  20. A. F. Horadam & A. G. Shannon. Ward’s Staudt-Clausen Problem. Mathemetica Scandinavica. 29 (1976): 239-250.
  21. P. A. Macmahon. Combinatory Analysis. Cambridge: Cambridge University Press, 1916.
  22. J. Riordan. An Introduction to Combinatorial Analysis. New York: Wiley, 1958, p.3.
  23. J. Riordan. A Note on a q-extension of Ballot Numbers. Journal of Combinatorial Theory. 4 (1968): 191-193.
  24. A. G. Shannon, Some Fermatian Special Functions, Notes on Number Theory & Discrete Mathematics, in press.
  25. G. J. Tee. Russian Peasant Multiplication and Egyptian Division in Zeckendorf Arithmetic. Australian Mathematical Society Gazette. 30 (2003): 267-276.
  26. M. Ward. A Calculus of Sequences. American Journal of Mathematics. 75 (1936): 255-266.

Related papers

Cite this paper

Shannon, A. G. (2004). Some properties of Fermatian numbers. Notes on Number Theory and Discrete Mathematics, 10(2), 25-33.

Comments are closed.