Some infinite series summations involving linear recurrence relations of order 2 and 3

Anthony G. Shannon, Peter J.-S. Shiue, Shen C. Huang, Ali Balooch, Yu-Chung Liu
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 2, Pages 283–310
DOI: 10.7546/nntdm.2024.30.2.283-310
Full paper (PDF, 319 Kb)

Details

Authors and affiliations

Anthony G. Shannon
Warrane College, University of New South Wales
Kensington, NSW 2033, Australia

Peter J.-S. Shiue
Department of Mathematical Sciences, University of Nevada, Las Vegas
4505 S Maryland Pkwy, Las Vegas, NV 89154, USA

Shen C. Huang
Department of Mathematical Sciences, University of Nevada, Las Vegas
4505 S Maryland Pkwy, Las Vegas, NV 89154, USA

Ali Balooch
Department of Mathematical Sciences, University of Nevada, Las Vegas
4505 S Maryland Pkwy, Las Vegas, NV 89154, USA

Yu-Chung Liu
School of Mathematical and Statistical Sciences, Clemson University
105 Sikes Hall, Clemson, SC 29634, USA

Abstract

This paper extends known results of second and third order recursive sequences through extensive formulations of properties of the roots of their characteristic equations, some are old but most are new. They are applied to novel studies of \sum_{n=0}^{\infty}{\frac{a_{mn}}{10^{n+1}}, \ m=1,2,3}, including their convergence criteria, and applied to many standard sequences, as particular cases of a generic \left\{a_n\right\}. The detailed development of the algebra of the pertinent theorems, and their associated lemmas and corollaries, should open up new vistas for interested number theorists with the concluding results on series values.

Keywords

  • Arithmetic sequence
  • Balancing sequence
  • Fermat sequence
  • Fibonacci sequence
  • Geometric sequence
  • Jacobsthal sequence
  • Leonardo sequence
  • Lucas sequence
  • Mersenne sequence
  • Padovan sequence
  • Pell sequence
  • Perrin sequence

2020 Mathematics Subject Classification

  • 11B39
  • 11A25

References

  1. Bicknell-Johnson, M., & Bergum, G. E. (1988). The generalized Fibonacci numbers 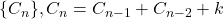\{C_n\}, {C}_n= {C}_{n-1}+ {C}_{n-2}+ k. In: Philippou, A. N., Horadam, A. F., Bergum, G. E. (Eds.). Applications of Fibonacci Numbers: Proceedings of The Second International Conference on Fibonacci Numbers and Their Applications, Springer, Dordrecht, pp. 193–205.
  2. Catarino, P. M. M. C., & Borges, A. (2019). On Leonardo numbers. Acta Mathematica Universitatis Comenianae, 89(1), 75–86.
  3. Gould, H. W. (1999). The Girard–Waring power sum formulas for symmetric functions, and Fibonacci sequences. The Fibonacci Quarterly, 37, 135–140.
  4. He, T.-X., & Shiue, P. J.-S. (2009). On sequences of numbers and polynomials defined by linear recurrence relations of order 2. International Journal of Mathematics and Mathematical Sciences, 2009, Article ID 709386.
  5. He, T.-X., Liao, H.-C., & Shiue, P. J.-S. (2018). Matrix representation of recursive sequences of order 3 and its applications. Journal of Mathematical Research with Applications, 38(3), 221–235.
  6. Horadam, A. F. (1967). Special properties of the sequence w_n (a, b; p, q). The Fibonacci Quarterly, 5(5), 424–434.
  7. Hudson, R. H. (1987). Convergence of Tribonacci decimal expansions. The Fibonacci Quarterly, 25, 163–170.
  8. Kuhapatanakul, K., & Chobsorn, J. (2022). On the generalized Leonardo numbers. Integers, 22, Article ID A48.
  9. Lidl, R., & Niederreiter, H. (1997). Finite Fields, 20. Cambridge University Press.
  10. Liu, Y.-C., & Shiue, P. J.-S. (2022). Convergent series of a second-order linear recursive sequence. Math Media, 44(3), 31–41 (In Chinese).
  11. Long, C. T. (1981). The decimal expansion of 1/89 and related results. The Fibonacci Quarterly, 19(1), 53–56.
  12. Melham, R. S, & Shannon, A. G. (1995). Some infinite series summations using power-series evaluated at a matrix. The Fibonacci Quarterly, 33(1), 13–20.
  13. Niven, I., Zuckerman, H. S., & Montgomery, H. L. (1991). An Introduction to the Theory of Numbers. John Wiley & Sons.
  14. Panda, G. K., & Ray, P. K. (2011). Some links of balancing and cobalancing numbers with Pell and associated Pell numbers. Bulletin of the Institute of Mathematics, Academia Sinica (New Series), 6(1), 41–72.
  15. Shannon, A. G., Anderson, P. G., & Horadam, A. F. (2006). Properties of Cordonnier, Perrin and van der Laan numbers. International Journal of Mathematical Education in Science and Technology, 37(7), 825–831.
  16. Shannon, A. G., Shiue, P. J.-S., & Huang, S. C. (2023). Notes on generalized and extended Leonardo numbers. Notes on Number Theory and  Discrete Mathematics, 29(4), 752–773.
  17. Sloane, N. J. A. (2008). The On-line Encyclopedia of Integer Sequences. Available online at: https://oeis.org.
  18. Ward, M. (1948). Memoir on elliptic divisibility sequences. American Journal of
    Mathematics, 70(1), 31–74.

Manuscript history

  • Received: 14 February 2023
  • Revised: 14 May 2024
  • Accepted: 18 May 2024
  • Online First: 19 May 2024

Copyright information

Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Related papers

Cite this paper

Shannon, A. G., Shiue, P. J.-S., Huang, S. C., Balooch, A., & Liu, Y.-C. (2024). Some infinite series summations involving linear recurrence relations of order 2 and 3. Notes on Number Theory and Discrete Mathematics, 30(2), 283-310, DOI: 10.7546/nntdm.2024.30.2.283-310.

Comments are closed.