E. Mehraban, Ö. Deveci, E. Hincal
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 2, Pages 271–282
DOI: 10.7546/nntdm.2024.30.2.271-282
Full paper (PDF, 302 Kb)
Details
Authors and affiliations
E. Mehraban ![]()
![]()
1 Mathematics Research Center, Near East University TRNC, Mersin 10, 99138 Nicosia, Turkey
2 Department of Mathematics, Near East University TRNC, Mersin 10, 99138 Nicosia, Turkey
3 Faculty of Art and Science, University of Kyrenia TRNC, Mersin 10, 99320 Kyrenia, Turkey
Ö. Deveci ![]()
![]()
Department of Mathematics, Faculty of Science and Letters, Kafkas University
36100, Turkey
E. Hincal ![]()
![]()
1 Mathematics Research Center, Near East University TRNC, Mersin 10, 99138 Nicosia, Turkey
2 Department of Mathematics, Near East University TRNC, Mersin 10, 99138 Nicosia, Turkey
3 Faculty of Art and Science, University of Kyrenia TRNC, Mersin 10, 99320 Kyrenia, Turkey
Abstract
The purpose of this paper is to determine the algebraic properties of finite groups via a Mersenne-like sequence. Firstly, we introduce the generalized order ![]() -Mersenne number sequences and study the periods of these sequences modulo
-Mersenne number sequences and study the periods of these sequences modulo ![]() . Then, we get some interesting structural results. Furthermore, we expand the generalized order
. Then, we get some interesting structural results. Furthermore, we expand the generalized order ![]() -Mersenne number sequences to groups and we give the definition of the generalized order
-Mersenne number sequences to groups and we give the definition of the generalized order ![]() -Mersenne sequences,
-Mersenne sequences, ![]() , in the
, in the ![]() -generator groups and also, investigate these sequences in the non-Abelian finite groups in detail. At last, we obtain the periods of the generalized order
-generator groups and also, investigate these sequences in the non-Abelian finite groups in detail. At last, we obtain the periods of the generalized order ![]() -Mersenne sequences in some special groups as applications of the results produced.
-Mersenne sequences in some special groups as applications of the results produced.
Keywords
- Period
- Mersenne number
- The generalized order
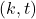 -Mersenne number sequences
-Mersenne number sequences  -group
-group
2020 Mathematics Subject Classification
- 20F05
- 11B39
- 20D60
References
- Bennett, M. A., Patel, V., & Siksek, S. (2019). Shifted powers in Lucas–Lehmer sequences. Research in Number Theory, 5(1), Article ID 15.
- Catarino, P., Campos, H., & Vasco, P. (2016). On the Mersenne sequence. Annales Mathematicae et Informaticae, 46, 37–53.
- Deveci, Ö., & Shannon, A. G. (2018). The quaternion-Pell sequence. Communications in Algebra, 46(12), 5403–5409.
- Doostie, H. & Hashemi, M. (2006). Fibonacci lengths involving the Wall number k(n). Journal of Applied Mathematics and Computing, 20(1–2), 171–180.
- Esmaeili, M., Moosavi, M., & Gulliver, T. A. (2017). A new class of Fibonacci sequence based error correcting codes. Cryptography and Communications, 9(3), 379–396.
- Falcon, S. (2013). On the generating matrices of the k-Fibonacci numbers. Proyecciones, 32(4), 347–357.
- Gautam, R. (2018). Balancing numbers and application. Journal of Advanced College of Engineering and Management, 4, 137–143.
- Goy, T. (2018). On new identities for Mersenne numbers. Applied Mathematics E-Notes, 18, 100–105.
- Hashemi, M., & Mehraban, E. (2021). The generalized order k-Pell sequences in some special groups of nilpotency class 2. Communications in Algebra, 50(4), 1768–1784.
- Hashemi, M., & Mehraban, E. (2023). Fibonacci length and the generalized order k-Pell sequences of the 2-generator p-groups of nilpotency class 2. Journal of Algebra and Its Applications, 22(3), Article ID 2350061.
- Jaroma, J. H., & Reddy, K. N. (2007). Classical and alternative approaches to the Mersenne and Fermat numbers. The American Mathematical Monthly, 114(8), 677–687.
- Koshy, T., & Gao, Z. (2013). Catalan numbers with Mersenne subscripts. Mathematical Scientist, 38(2), 86–91.
- Ochalik, P., & Wloch, A. (2018). On generalized Mersenne numbers, their interpretations and matrix generators. Annales Universitatis Mariae Curie-Skłodowska. Section A, 1, 69–76.
- Osipov, D. V. (2015). The discrete Heisenberg group and its automorphism group. Mathematical Notes, 98(1–2), 185–188.
- Prasad, K., & Mahato, H. (2022). Cryptography using generalized Fibonacci matrices with Affine-Hill cipher. Journal of Discrete Mathematical Sciences and Cryptography, 25(8), 2341–2352.
- Shannon, A. G., Erdağ, O., & Deveci, Ö. (2021). On the connections between Pell numbers and Fibonacci p-numbers. Notes on Number Theory and Discrete Mathematics, 21(1), 148–160.
- Stakhov, A. P. (2006). Fibonacci matrices, a generalization of the Cassini formula and new coding theory. Chaos, Solitions & Fractals, 30(1), 56–66.
- Taşci, D., Tuğlu, N., & Asci, M. (2011). On Fibo–Pascal matrix involving k-Fibonacci and k-Pell matrices. Arabian Journal for Science and Engineering, 36, 1031–1037.
Manuscript history
- Received: 22 February 2023
- Revised: 11 May 2024
- Accepted: 15 May 2024
- Online First: 17 May 2024
Copyright information
![]() Ⓒ 2024 by the Authors.
Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Shannon, A. G., Erdağ, O., & Deveci, Ö. (2021). On the connections between Pell numbers and Fibonacci p-numbers. Notes on Number Theory and Discrete Mathematics, 21(1), 148–160.
Cite this paper
Mehraban, E., Deveci, Ö., & Hincal, E. (2024). The generalized order (k,t)-Mersenne sequences in groups. Notes on Number Theory and Discrete Mathematics, 30(2), 271-282, DOI: 10.7546/nntdm.2024.30.2.271-282.


