József Sándor
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 1, Pages 111–115
DOI: 10.7546/nntdm.2024.30.1.111-115
Full paper (PDF, 210 Kb)
Details
Authors and affiliations
József Sándor ![]()
![]()
Department of Mathematics, Babeș-Bolyai University
Str. Kogalniceanu 1, 400084 Cluj-Napoca, Romania
Abstract
We study the arithmetical products ![]() ,
, ![]() and
and ![]() , where
, where ![]() runs through the divisors of an integer
runs through the divisors of an integer ![]()
Keywords
- Arithmetic functions
- Inequalities for arithmetic functions
- Inequalities for sums
2020 Mathematics Subject Classification
- 11A25
- 11N37
- 26D15
References
- Cartwright, D. I., & Field, M. J. (1978). A refinement of the arithmetic mean-geometric mean inequality. Proceedings of the American Mathematical Society, 71(1), 36–38.
- Erdős, P., & Zaremba, S. K. (1973). The arithmetic function
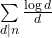 . Demonstratio Mathematica, 6, 575–579.
. Demonstratio Mathematica, 6, 575–579. - Mitrinović, D. S. (1970). Analytic Inequalities. Springer Verlag.
- Sándor, J., Mitrinović, D. S., & Crstici, B. (2006). Handbook of Number Theory I. Springer.
Manuscript history
- Received: 3 August 2023
- Revised: 12 February 2024
- Accepted: 28 February 2024
- Online First: 6 March 2024
Copyright information
![]() Ⓒ 2024 by the Author.
Ⓒ 2024 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Sándor, J. (2024). On certain arithmetical products involving the divisors of an integer. Notes on Number Theory and Discrete Mathematics, 30(1), 111-115, DOI: 10.7546/nntdm.2024.30.1.111-115.


