n-Rooks and n-queens problem on planar and modular chessboards with hexagonal cells

Eduard C. Taganap and Rainier D. Almuete
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 4, Pages 774–788
DOI: 10.7546/nntdm.2023.29.4.774-788
Full paper (PDF, 2044 Kb)

Details

Authors and affiliations

Eduard C. Taganap
Department of Mathematics and Physics, Central Luzon State University
Science City of Muñoz, Nueva Ecija, Philippines

Rainier D. Almuete
Department of Statistics, Central Luzon State University
Science City of Muñoz, Nueva Ecija, Philippines

Abstract

We show the existence of solutions to the -rooks problem and -queens problem on chessboards with hexagonal cells, problems equivalent to certain three and six direction riders on ordinary chessboards. Translating the problems into graph theory problems, we determine the independence number (maximum size of independent set) of rooks graph and queens graph. We consider the planar diamond-shaped H with hexagonal cells, and the board H as a flat torus T. Here, a rook can execute moves on lines perpendicular to the six sides of the cell it is placed, and a queen can execute moves on those lines together with lines through the six corners of the cell it is placed.

Keywords

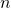• -Queens problem
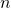• -Rooks problem
• Non-attacking fairy chess riders
• Queens graph
• Rooks graph
• Independent sets

2020 Mathematics Subject Classification

• 05C69
• 05C99

References

1. Bell, J., & Stevens, B. (2009). A survey of known results and research areas for n-queens. Discrete Mathematics, 309(1), 1–31.
2. Bezzel, M. (1848). Proposal of 8-queens problem. Berliner Schachzeitung, 3, 363.
   Submitted under the author name “Schachfreund”.
3. Bueno, A. C. (2013). On the n non-attacking queens problem. International Journal of Advanced Mathematical Sciences, 1(2), 50–55.
4. Burger, A. P., Mynhardt, C. M., & Cockayne, E. J. (2001). Queens graphs for chessboards on the torus. Australasian Journal of Combinatorics, 24, 231–246.
5. Burger, A. P., Mynhardt, C. M., & Weakley, W. D. (2003). The domination number of the toroidal queens graph of size 3k × 3k. Australasian Journal of Combinatorics, 28, 137–148.
6. Cairns, G. (2002). Pillow chess. Mathematics Magazine, 75(3), 173–186.
7. Cairns, G. (2004). Queens on non-square tori. Electronic Journal of Combinatorics, 8, 6.
8. DeMaio, J., & Lien Tran, H. (2013). Domination and independence on a triangular honeycomb chessboard. The College Mathematics Journal, 44(4), 307–314.
9. Fricke, G. H., Hedetniemi, S. M., Hedetniemi, S. T., McRae, A. A., Wallis, C. K., Jacobson, M. S., Martin, H. W., & Weakley, W. D. (1995). Combinatorial problems on chessboards: A brief survey. Graph Theory, Combinatorics, and Algorithms, Vol. 1, 2 (Kalamazoo, MI, 1992), Wiley-Intersci. Publ., Wiley, New York, 507–528.
10. Harborth, H., Kultan, V., Nyaradyova, K., & Spendelova, Z. (2003). Independence on triangular hexagon boards. Proceedings of the Thirty-Fourth Southeastern International Conference on Combinatorics, Graph Theory and Computing, Vol. 160, 215–222.
11. Jelliss, G. P. (2019). Knight’s Tour Notes (Theory of Moves). GPJ Publications. Available online at: https://www.mayhematics.com/p/p.htm.
12. Kotěšovec, V. (2013). Non-Attacking Chess Pieces (6th ed.). Available online at:  http://www.kotesovec.cz/books/kotesovec_non_attacking_chess_pieces_2013_6ed.pdf.
13. Monsky, P. (1989). Problem E3162, American Mathematical Monthly, 96, 258–259.
14. Nudelman, S. P. (1995). The modular n-queens problem in higher dimensions. Discrete Mathematics, 146(1–3), 159–167.
15. Polya, G. (1918). Uber die “doppelt-periodischen” los ungen des n-damen-problems. Mathematische Unterhaltungen und Spiele, Vol. 2 (2nd ed.). B.G. Teubner, 364–374.
16. Pritchard, D. B., & Beasley, J. D. (2007). The Classified Encyclopedia of Chess Variants, 203–212. Available online at: https://www.jsbeasley.co.uk/encyc/encyc.pdf.
17. Sloane, N. J. A. (1964). The On-Line Encyclopedia of Integer Sequences. Available online at: https://oeis.org/A099152.
18. Theron, W. F. D., & Geldenhuys, G. (1998). Domination by queens on a square beehive. Discrete Mathematics, 178(1–3), 213–220.
19. Wagon, S. (2014). Graph theory problems from hexagonal and traditional chess. The College Mathematics Journal, 45(4), 278–287.
20. Watkins, J. J. (2004). Across the Board: The Mathematics of Chessboard Problems. Princeton University Press, Princeton, NJ.

Manuscript history

• Received: 17 June 2022
• Revised: 27 July 2023
• Accepted: 25 November 2023
• Online First: 27 November 2023

Copyright information

Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).