Bishnu Paudel and Chris Pinner
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 3, Pages 603–619
DOI: 10.7546/nntdm.2023.29.3.603-619
Full paper (PDF, 293 Kb)
Details
Authors and affiliations
Bishnu Paudel ![]()
Department of Mathematics, Kansas State University
Manhattan KS 66506, United States
Chris Pinner ![]()
Department of Mathematics, Kansas State University
Manhattan KS 66506, United States
Abstract
Let ![]() denote the cyclic group of order
denote the cyclic group of order ![]() . We show how the group determinant for
. We show how the group determinant for ![]() can be simply written in terms of the group determinant for
can be simply written in terms of the group determinant for ![]() . We use this to get a complete description of the integer group determinants for
. We use this to get a complete description of the integer group determinants for ![]() where
where ![]() is the dihedral group of order
is the dihedral group of order ![]() , and
, and ![]() where
where ![]() is the quaternion group of order
is the quaternion group of order ![]() .
.
Keywords
- Integer group determinant
- Dihedral group
- Quaternion group
2020 Mathematics Subject Classification
- 11C20
- 15B36
- 11C08
- 43A40
References
- Boerkoel, T., & Pinner, C. (2018). Minimal group determinants and the Lind–Lehmer problem for dihedral groups. Acta Arithmetica, 186(4), 377–395.
- Conrad, K. (1998). The origin of representation theory. L’Enseignement Mathématique, 44(3–4), 361–392.
- DeSilva, D., Mossinghoff, M., Pigno, V., & Pinner, C. (2019). The Lind–Lehmer constant for certain p-groups. Mathematics of Computation, 88(316), 949–972.
- DeSilva, D., & Pinner, C. G. (2014). The Lind–Lehmer constant for
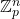 . Proceedings of the American Mathematical Society, 142, 1935–1941.
. Proceedings of the American Mathematical Society, 142, 1935–1941. - Frobenius, F. G. (1968). Über die Primefactoren der Gruppendeterminante. Gesammelte Ahhand-lungen, Band III. Springer, New York, pp. 38–77. MR0235974.
- Johnson, K. W. (2019). Group Matrices Group Determinants and Representation Theory. Lecture Notes in Mathematics, 2233, Springer, Cham.
- Laquer, H. T. (1980). Values of circulants with integer entries. A Collection of Manuscripts Related to the Fibonacci Sequence. Fibonacci Association, Santa Clara, pp. 212–217. MR0624127.
- Mahoney, M. K. (1982). Determinants of integral group matrices for some nonabelian 2-generator groups. Linear and Multilinear Algebra, 11(2), 189–201.
- Mahoney, M. K., & Newman, M. (1980). Determinants of abelian group matrices. Linear and Multilinear Algebra, 9(2), 121–132.
- Mossinghoff, M., & Pinner, C. (2023). Prime power order circulant determinants. Illinois Journal of Mathematics, 67(2), 333–362.
- Newman, M. (1980). On a problem suggested by Olga Taussky-Todd. Illinois Journal of Mathematics, 24, 156–158.
- Newman, M. (1980). Determinants of circulants of prime power order. Linear Multilinear Algebra, 9(3), 187–191. MR0601702.
- Paudel, B., & Pinner, C. (2022). Integer circulant determinants of order
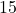 . Integers, 22, Article A4.
. Integers, 22, Article A4. - Pinner, C., & Smyth, C. (2020). Integer group determinants for small groups. The
Ramanujan Journal, 51(2), 421–453. - Taussky-Todd, O. (1977). Integral group matrices. Notices of the American Mathematical Society, 24(3), A-345. (Abstract no. 746-A15, 746th Meeting, Hayward, CA, Apr. 22–23, 1977).
- Yamaguchi, N., & Yamaguchi, Y. (2022). Generalized Dedekind’s theorem and its
application to integer group determinants. arXiv: 2203.14420v2 [math.RT]. - Yamaguchi, N., & Yamaguchi, Y. (2023). Remark on Laquer’s theorem for circulant determinants. International Journal of Group Theory, 12(4), 265–269.
- Yamaguchi, Y., & Yamaguchi, N. (2022). Integer group determinants for
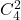 . arXiv: 2211.01597 [math.NT].
. arXiv: 2211.01597 [math.NT]. - Yamaguchi, Y., & Yamaguchi, N. (2022). Integer group determinants for abelian groups of order
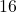 , arXiv: 2211.14761 [math.NT].
, arXiv: 2211.14761 [math.NT]. - Yamaguchi, Y., & Yamaguchi, N. (2023). Integer group determinants for
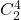 . The Ramanujan Journal, DOI: 10.1007/s11139-023-00727-z.
. The Ramanujan Journal, DOI: 10.1007/s11139-023-00727-z. - Yamaguchi, Y., & Yamaguchi, N. (2023). Integer circulant determinants of order
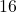 . The Ramanujan Journal, 61, 1283–1294.
. The Ramanujan Journal, 61, 1283–1294.
Manuscript history
- Received: 22 March 2023
- Revised: 4 August 2023
- Accepted: 11 August 2023
- Online First: 25 August 2023
Copyright information
![]() Ⓒ 2023 by the Authors.
Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Paudel, B, & Pinner, C. (2023). The group determinants for ℤn × H. Notes on Number Theory and Discrete Mathematics, 29(3), 603-619, DOI: 10.7546/nntdm.2023.29.3.603-619.


