Pentti Haukkanen
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 2, Pages 185–194
DOI: 10.7546/nntdm.2023.29.2.185-194
Full paper (PDF, 189 Kb)
Details
Authors and affiliations
Pentti Haukkanen ![]()
![]()
Faculty of Information Technology and Communication Sciences,
FI-33014 Tampere University, Finland
Abstract
We study existence of a solution of the arithmetical equation ![]() in
in ![]() where
where ![]() is the Dirichlet convolution of arithmetical functions
is the Dirichlet convolution of arithmetical functions ![]() and
and ![]() and derive an explicit expression for the solution. As applications we obtain expressions for the Möbius function
and derive an explicit expression for the solution. As applications we obtain expressions for the Möbius function ![]() and the so-called totients. As applications we also present our results on the arithmetical equation
and the so-called totients. As applications we also present our results on the arithmetical equation ![]() in the language of Cauchy convolution and further deconvolution in discrete linear systems.
in the language of Cauchy convolution and further deconvolution in discrete linear systems.
Keywords
- Arithmetical equation
- Dirichlet convolution
- Möbius function
- Totient function
- Cauchy convolution
- Discrete linear system
2020 Mathematics Subject Classification
- 11A25
References
- Amante, S. (1937). Sul quoziente integrale di due funzioni numeriche nel caso singolare. Atti dell’Accademia di Scienze, Lettere e Arti di Palermo, 20, 15–17.
- Baustian, F., & Bobkov, V. (2020). On asymptotic behavior of Dirichlet inverse.
International Journal of Number Theory, 16(06), 1337–1354. - Beumer, M. G. (1962). The arithmetical function
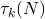 . American Mathematical Monthly, 69, 777–781.
. American Mathematical Monthly, 69, 777–781. - Feckan, M. (2008). Note on arithmetic convolution equations. Proceedings of the American Mathematical Society, 136(2), 453–459.
- Gabel, R. A., & Roberts, R. A. (1987). Signals and Linear Systems (3rd ed.). John Wiley & Sons, New York.
- Glöckner, H., Lucht, L., & Porubský, Š. (2007). Solutions to arithmetic convolution equations. Proceedings of the American Mathematical Society, 135(6), 1619–1629.
- Haukkanen, P. (1988). Arithmetical equations involving semi-multiplicative functions and the Dirichlet convolution. Rendiconti di Matematica e delle sue Applicazioni, (7)8, 511–517.
- Haukkanen, P. (1989). On the Davison convolution of arithmetical functions. Canadian Mathematical Bulletin, 32(4), 467–473.
- Haukkanen, P. (1996). Some characterizations of totients. International Journal of Mathematics and Mathematical Sciences, 19(2), 209–217.
- Haukkanen, P. (2000). Expressions for the Dirichlet inverse of arithmetical functions. Notes on Number Theory and Discrete Mathematics, 6(4), 118–124.
- Haukkanen, P. (2000). On a generalized convolution of incidence functions. Discrete Mathematics, 215(1-3), 103–113.
- Haukkanen, P. (2012). Extensions of the class of multiplicative functions. East–West Journal of Mathematics, 14(2), 101–113.
- Jackson, L. B. (1989). Digital Filters and Signal Processing (2nd ed.). Kluwer, Boston.
- Laohakosol, V., & Pabhapote, N. (2005). Properties of rational arithmetic functions. International Journal of Mathematics and Mathematical Sciences, 2005(24), 3997–4017.
- McCarthy, P. J. (1979). Introduction to Arithmetical Functions. Springer–Verlag, New York.
- Pellegrino, F. (1963). La divisione integrale. Rendiconti di Matematica e delle sue
Applicazioni, 22(5), 489–497. - Quinton, P., & Robert, Y. (1992). Systolic convolution of arithmetic functions. Theoretical Computer Science, 95(2), 207–229.
- Sándor, J., & Atanassov, K. T. (2021). Arithmetic Functions. Nova Science Publishers.
- Sándor, J., & Crstici, P. (2004). Handbook of Number Theory II. Kluwer Academic.
- Sivaramakrishnan, R. (1989). Classical Theory of Arithmetic Functions. In: Monographs and Textbooks in Pure and Applied Mathematics, Vol. 126. Marcel Dekker, New York.
- Srisopha, S., Ruengsinsub, P., & Pabhapote, N. (2012). The
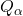 -convolution of arithmetic functions and some of its properties. East–West Journal of Mathematics, 14(01), 76–83.
-convolution of arithmetic functions and some of its properties. East–West Journal of Mathematics, 14(01), 76–83. - Succi, F. (1956). Sulla espressione del quoziente integrale di due funzioni aritmetiche. Rendiconti di Matematica e delle sue Applicazioni, 15(5), 80–92.
Manuscript history
- Received: 30 January 2023
- Revised: 11 March 2023
- Accepted: 22 March 2023
- Online First: 3 April 2023
Copyright information
![]() Ⓒ 2023 by the Author.
Ⓒ 2023 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Haukkanen, P. (2025). Identical equations for multiplicative functions. Notes on Number Theory and Discrete Mathematics, 31(2), 289-298.
- Haukkanen, P. (2024). Quotients of sequences under the binomial convolution. Notes on Number Theory and Discrete Mathematics, 30(4), 681-690.
- Haukkanen, P. (2000). Expressions for the Dirichlet inverse of arithmetical functions. Notes on Number Theory and Discrete Mathematics, 6(4), 118–124.
Cite this paper
Haukkanen, P. (2023). Quotients of arithmetical functions under the Dirichlet convolution. Notes on Number Theory and Discrete Mathematics, 29(2), 185-194, DOI: 10.7546/nntdm.2023.29.2.185-194.


