Identities involving some special numbers and polynomials on p-adic integral

Neşe Ömür, Sibel Koparal, Ömer Duran and Kübra Nur Südemen
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 3, Pages 564–574
DOI: 10.7546/nntdm.2022.28.3.564-574
Full paper (PDF, 192 Kb)

Details

Authors and affiliations

Neşe Ömür
Department of Bioinformatics and Mathematical Modelling,
Department of Mathematics, University of Kocaeli
41380 Izmit, Kocaeli, Turkey

Sibel Koparal
Department of Bioinformatics and Mathematical Modelling,
Department of Mathematics, University of Kocaeli
41380 Izmit, Kocaeli, Turkey

Ömer Duran
Department of Bioinformatics and Mathematical Modelling,
Department of Mathematics, University of Kocaeli
41380 Izmit, Kocaeli, Turkey

Kübra Nur Südemen
Department of Bioinformatics and Mathematical Modelling,
Department of Mathematics, University of Kocaeli
41380 Izmit, Kocaeli, Turkey

Abstract

In this paper, we get new identities involving Bernoulli, Daehee and Stirling numbers, and their representations by using p-adic integrals and combinatorial techniques.

Keywords

• p-adic integral
• q-Bernoulli numbers
• Generating functions

2020 Mathematics Subject Classification

• 05A15
• 11S80
• 11B68

References

1. Duran, Ö., Ömür, N., & Koparal, S. (2020). On sums with generalized harmonic, hyperharmonic and special numbers. Miskolc Mathematical Notes, 21(2), 791–803.
2. Euler, L. (1748). Introductio in Analysin in Nitorum. Apud Marcum-Michaelem Bousquet & Socios.
3. Genčev, M. (2011). Binomial sums involving harmonic numbers. Mathematica Slovaca, 61(2), 215–226.
4. Jang, L.-C., Kim, D. S., Kim, T. & Lee, H. (2020). p-adic integral on ℤ_p associated with degenerate Bernoulli polynomials of the second kind. Advances in Difference Equations, Article ID 278.
5. Kim, T., Kim, D. S., Jang, L.-C., Lee, H. & Kim, H. (2022). Representations of degenerate Hermite polynomials. Advances in Applied Mathematics, 139, Article ID 102359.
6. Kim, D. S., Kim, T., Lee, S. H., & Seo, J. J. (2014). Higher-order Daehee numbers and polynomials. International Journal of Mathematical Analysis, 8(6), 273–283.
7. Kim, D. S., Kim, T., Kwon, J., Lee, S.-H., & Park, S. (2021). On λ-linear functionals arising from p-adic integrals on ℤ_p. Advances in Continuous and Discrete Models, 2021, Article ID 479.
8. Kim, T. (2007). A note on p-adic q-integral on ℤ_p associated with q-Euler numbers. Advanced Studies in Contemporary Mathematics, 15, 133–137.
9. Kim, T. (2006). A note on some formulae for the q-Euler numbers and polynomials. Proceedings of the Jangjeon Mathematical Society, 9(2), 227–232.
10. Kim, T. (2012). Lebesgue–Radon–Nikodym theorem with respect to fermionic p-adic invariant measure on ℤ_p. Russian Journal of Mathematical Physics, 19(2), 193–196.
11. Kim, T. (2016). On degenerate q-Bernoulli polynomials. Bulletin of the Korean Mathematical Society, 53(4), 1149–1156.
12. Kim, T. (2002). q-Volkenborn integration. Russian Journal of Mathematical Physics, 9(3), 288–299.
13. Kim, T. (2009). Some identities on the q-Euler polynomials of higher order and q-Stirling numbers by the fermionic p-adic integral on ℤ_p. Russian Journal of Mathematical Physics, 16(4), 484–491.
14. Lee, J. G., & Kwon, J. (2017). The modified degenerate q-Bernoulli polynomials arising from p-adic invariant integral on ℤ_p. Advances in Difference Equations, 2017, Article ID 29.
15. Ma, Y., Kim, T., Kim, D. S., & Lee, H. (2022). Study on q-analogues of Catalan–Daehee numbers and polynomials. Filomat, 36(5), 1499–1506.
16. Ömür, N., & Bilgin, G. (2018). Some applications of the generalized hyperharmonic numbers of order 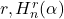. Advances and Applications in Mathematical Sciences, 17(9), 617–627.
17. Ömür, N., Südemen, K. N., & Koparal, S.  Some identities with special numbers (submitted).
18. Park, J. W. (2015). On the q-analogue of λ-Daehee polynomials. Journal of Computational Analysis and Applications, 19(6), 966–974.
19. Yun, S. J., & Park, J.-W. (2020). On fully degenerate Daehee numbers and polynomials of the second kind. Journal of Mathematics, 2020, Article ID 7893498.

Manuscript history

• Received: 16 March 2022
• Revised: 5 August 2022
• Accepted: 14 September 2022
• Online First: 27 September 2022