B. M. Phong and R. B. Szeidl
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 2, Pages 240–251
DOI: 10.7546/nntdm.2022.28.2.240-251
Full paper (PDF, 192 Kb)
Details
Authors and affiliations
B. M. Phong ![]()
![]()
Department of Computer Algebra, University of Eötvös Loránd
1117 Budapest, Hungary
R. B. Szeidl ![]()
Department of Computer Algebra, University of Eötvös Loránd
1117 Budapest, Hungary
Abstract
We give all solutions ![]() of the functional equation
of the functional equation
![]()
where ![]() .
.
Keywords
- Arithmetical function
- Functional equation
- Dirichlet character
2020 Mathematics Subject Classification
- 11A07
- 11A25
- 11N25
- 11N64
References
- De Koninck, J.-M., Kátai, I., & Phong, B. M. (1997). A new characteristic of the identity function. Journal of Number Theory, 63(2), 325–338.
- Khanh, B. M. M. (2021). Characterization of the identity function with an equation function. Annales Universitatis Scientiarium Budapestinensis de Rolando Eötvös Nominatae. Sectio Computatorica, 52, 195–216.
- Park, P.-S. (in press). Multiplicative functions commutable with binary quadratic forms
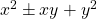 . Bulletin of the Korean Mathematical Society.
. Bulletin of the Korean Mathematical Society. - Phong, B. M. (2006). A characterization of the identity function with the equation of Hosszú type. Publicationes Mathematicae Debrecen, 69(1–2), 219–226.
- Phong, B. M. (2016). A characterization of identity with function equation II. Acta Mathematica Hungarica, 148(2), 450–465.
- Phong, B. M., & Szeidl, R. B. (2021). On the equation
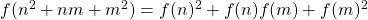 . Annales Universitatis Scientiarium Budapestinensis de Rolando Eötvös Nominatae. Sectio Computatorica, 52, 255–278.
. Annales Universitatis Scientiarium Budapestinensis de Rolando Eötvös Nominatae. Sectio Computatorica, 52, 255–278. - Spiro, C. (1992). Additive uniqueness set for arithmetic functions. Journal of Number Theory, 42, 232–246.
Manuscript history
- Received: 29 August 2021
- Revised: 23 April 2022
- Accepted: 28 April 2022
- Online First: 29 April 2022
Related papers
Cite this paper
Phong, B. M., & Szeidl, R. B. (2022). On the equation f(n2 − Dnm + m2) = f2(n) − Df(n)f(m) + f2(m). Notes on Number Theory and Discrete Mathematics, 28(2), 240-251, DOI: 10.7546/nntdm.2022.28.2.240-251.


