On k-circulant matrices with the generalized third-order Pell numbers

Yüksel Soykan
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 27, 2021, Number 4, Pages 187–206
DOI: 10.7546/nntdm.2021.27.4.187-206
Full paper (PDF, 265 Kb)

Details

Authors and affiliations

Yüksel Soykan
Department of Mathematics, Art and Science Faculty,
Zonguldak Bulent Ecevit University
67100, Zonguldak, Turkey

Abstract

In this paper, we obtain explicit forms of the sum of entries, the maximum column sum matrix norm, the maximum row sum matrix norm, Euclidean norm, eigenvalues and determinant of k-circulant matrix with the generalized third-order Pell numbers. We also study the spectral norm of this k-circulant matrix. Furthermore, some numerical results for demonstrating the validity of the hypotheses of our results are given.

Keywords

• Third-order Pell numbers
• Circulant matrix
• k-circulant matrix
• Tribonacci numbers
• Norm
• Spectral norm
• Determinant

2020 Mathematics Subject Classification

• 11B39
• 11B83
• 15A18
• 15A60
• 15B36
• 11C20

References

1. Alptekin, E. G. (2005). Pell, Pell–Lucas ve Modified Pell sayıları ile tanımlı circulant ve semicirculant matrisler. [PhD thesis, Selcuk Universitesi Fen Bilimleri Enstitusu]. Selcuk University Digital Archive. Retrieved from: http://hdl.handle.net/123456789/5959
2. Cline, R. E., Plemmons, R. J., & Worm, G. (1974). Generalized Inverses of Certain Toeplitz Matrices. Linear Algebra and its Applications 8, 25–33.
3. Coskun, A., & Taskara, N. (2018). On the Some Properties of Circulant Matrices with Third Order Linear Recurrent Sequences. Mathematical Sciences and Applications E-Notes, 6(1), 12–18.
4. Davis, P. J. (1979). Circulant Matrices, John Wiley & Sons, New York.
5. Deveci, O., Karaduman, E., & Campbell, C. M. (2007). The Fibonacci-Circulant Sequences and Their Applications. Iranian Journal of Science and Technology Transaction A-Science, 41(A4), 1033–1038.
6. Deveci, O. (2018). On The Fibonacci-Circulant p-Sequences. Utilitas Mathematica, 108, 107–124.
7. Horn, R. A., & Johnson, C. R. (2012). Matrix Analysis, Cambridge University Press, Cambridge, 2nd edition.
8. Horn, R. A., & Johnson, C. R. (1991). Topics in Matrix Analysis, Cambridge University Press, Cambridge.
9. Kızılateş, C., & Tuglu, N. (2018). On the Norms of Geometric and Symmetric Geometric Circulant Matrices with the Tribonacci Number. Gazi University Journal of Science, 31(2), 555–567.
10. Kızılateş, C., & Tuglu, N. (2016). On the Bounds for the Spectral Norms of Geometric Circulant Matrices. Journal of Inequalities and Applications, 2016(1), Article ID 312.
11. Ozkoc, A., & Ardıyok, E. (2016). Circulant and Negacyclic Matrices Via Tetranacci Numbers. Honam Mathematical Journal, 38(4), 725–738.
12. Pacheenburawana, A., & Sintunavarat, W. (2018). On the Spectral Norms of r-Circulant Matrices with the Padovan and Perrin Sequences. Journal of Mathematical Analysis, 9(3), 110–122.
13. Pethe, S. (1988). Some Identities for Tribonacci sequences. The Fibonacci Quarterly, 26(2), 144–151.
14. Polatlı, E. (2019). On the Bounds for the Spectral Norms of r-Circulant Matrices with a Type of Catalan Triangle Numbers. Journal of Science and Arts, 3(48), 575–578.
15. Radicic, B. (2019). On k-Circulant Matrices Involving the Jacobsthal Numbers. Revista De La Union Matematica Argentina, 60(2), 431–442.
16. Raza, Z., Riaz, M., & Ali, M. A. (2015). Some Inequalities on the Norms of Special Matrices with Generalized Tribonacci and Generalized Pell–Padovan Sequences. arXiv, http://arxiv.org/abs/1407.1369v2.
17. Raza, Z., & Ali, M. A. (2014). On the Norms of Circulant, r-Circulant, Semi-Circulant and Hankel Matrices with Tribonacci Sequence. arXiv, http://arxiv.org/abs/1407.1369v1.
18. Sintunavarat, W. (2016). The Upper Bound Estimation for the Spectral Norm of r-Circulant and Symmetric r-Circulant Matrices with the Padovan Sequence, Journal of Nonlinear Sciences and Applications, 9, 92–101.
19. Sloane, N. J. A. The on-line encyclopedia of integer sequences. Available online at: http: //oeis.org/.
20. Soykan Y. (2020). Generalized Tribonacci Numbers: Summing Formulas. International Journal of Advances in Applied Mathematics and Mechanics, 7(3), 57–76.
21. Soykan Y. (2020). A Study On Generalized (r,s,t)-Numbers. MathLAB Journal, 7, 101–129.
22. Soykan, Y. (2019). On Generalized Third-Order Pell Numbers. Asian Journal of Advanced Research and Reports, 6(1), 1–18.
23. Soykan, Y. (2020). A Closed Formula for the Sums of Squares of Generalized Tribonacci numbers. Journal of Progressive Research in Mathematics, 16(2), 2932–2941.
24. Soykan, Y. (2020). On the Sums of Squares of Generalized Tribonacci Numbers: Closed Formulas of 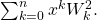Archives of Current Research International, 20(4), 22–47.
25. Soykan, Y. (2020). Summing Formulas For Generalized Tribonacci Numbers. Universal Journal of Mathematics and Applications, 3(1), 1–11.
26. Soykan, Y. (2021). A Study On the Sums of Squares of Generalized Tribonacci Numbers: Closed Form Formulas of 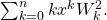Journal of Scientific Perspectives, 5(1), 1–23.
27. Soykan, Y. (2020). A Study on Sum Formulas for Generalized Tribonacci Numbers: Closed Forms of the Sum Formulas 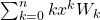and 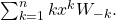Journal of Progressive Research in Mathematics, 17(1), 1–40.
28. Soykan, Y. (2020). Formulae For The Sums of Squares of Generalized Tribonacci Numbers: Closed Form Formulas of 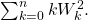IOSR Journal of Mathematics, 16(4), 1–18.
29. Soykan, Y. (2020). On Sum Formulas for Generalized Tribonacci Sequence. Journal of Scientific Research & Reports, 26(7), 27–52.
30. Tuglu, N., & Kızılateş, C. (2015). On the Norms of Circulant and r-Circulant Matrices with the Hyperharmonic Fibonacci Numbers. Journal of Inequalities and Applications, 2015, Article ID 253.
31. Turkmen, R., & Gokbas, H. (2016). On the Spectral Norm of r-Circulant Matrices with the Pell and Pell–Lucas Numbers. Journal of Inequalities and Applications, 2016, Article ID 65.
32. Uygun, S. (2016). Some Bounds for the Norms of Circulant Matrices with the k-Jacobsthal and k-Jacobsthal Lucas Numbers. Journal of Mathematics Research, 8(6), 133–138.
33. Uygun, Ş. & Yaşamalı, S. (2017). On the Bounds for the Norms of Circulant Matrices with the Jacobsthal and Jacobsthal–Lucas Numbers. Notes on Number Theory and Discrete Mathematics, 23(1), 91–98.
34. Uygun, Ş. & Yaşamalı, S. (2017). On the Bounds for the Norms of r-Circulant Matrices with the Jacobsthal and Jacobsthal–Lucas Numbers. International Journal of Pure and Applied Mathematics, 112(1), 93–102.
35. Zielke, G. (1988). Some Remarks on Matrix Norms, Condition Numbers, and Error Estimates for Linear Equations. Linear Algebra and its Applications, 110, 29–41.