A generalization to almost balancing and cobalancing numbers using triangular numbers

S. G. Rayaguru and G. K. Panda
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 26, 2020, Number 3, Pages 135–148
DOI: 10.7546/nntdm.2020.26.3.135-148
Full paper (PDF, 324 Kb)

Details

Authors and affiliations

S. G. Rayaguru
Department of Mathematics, National Institute of Technology
Rourkela, India

G. K. Panda
Department of Mathematics, National Institute of Technology
Rourkela, India

Abstract

A generalization of almost balancing numbers is studied using triangular numbers as the difference between the left and right hand sides of the defining equation of balancing numbers. In case of almost balancing numbers, this difference is kept 1; which is the first triangular number. Some specific representations of these numbers in terms of balancing and balancing related numbers are established and few more results with triangular, square triangular, balancing and balancing related numbers are also studied so as to generalize the identities obtained by A. Tekcan.

Keywords

• Balancing numbers
• Cobalancing numbers
• Almost balancing numbers
• Lucas-balancing numbers
• Lucas-cobalancing numbers
• Triangular numbers

2010 Mathematics Subject Classification

• 11B39
• 11B38

References

1. Behera, A., & Panda, G. K. (1999). On the square roots of triangular numbers, Fib. Quart., 37 (2), 98–105.
2. Dash, K. K., Ota, R. S., & Dash, S. (2012). 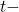balancing Numbers, Int. J. Contemp. Math. Sciences, 7 (41), 1999–2012.
3. Davala, R. K., & Panda, G. K. (2016) Supercobalancing Numbers, Matematika, 32 (1), 31–42.
4. Davala, R. K., & Panda, G. K. (2018). Subbalancing Numbers, Matematika, 34 (1), 163–172.
5. Gözeri, G. K., Özkoç, A., & Tekcan, A. (2017) Some Algebraic Relations on Balancing Numbers, Utilitas Mathematica, 103, 217–236.
6. Keskin, R., & Karaatlı, O. (2012). Some New Properties of Balancing Numbers and Square Triangular Numbers, J. Int. Seq., 15, Article 12.1.4.
7. Kovács, T., Liptai, K., & Olajos, P. (2010). On 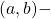balancing Numbers, Publ. Math. Deb., 77 (3–4), 485–498.
8. Liptai, K., Luca, F., Pinter, A., & Szalay, L. (2009). On Generalized Balancing Numbers, Indag. Mathem., 20 (1), 87–100.
9. Mollin, R. A. (2004). Fundamental Number Theory with Applications, Boca Raton, CRC press, London.
10. Olajos, P. (2010). Properties of Balancing, Cobalancing and Generalized Balancing Numbers, Annales Math. Info., 37, 125–138.
11. Özkoç, A., Tekcan, A., & Gözeri, G. K. (2017). Triangular and Square Triangular Numbers Involving Generalized Pell Numbers, Utilitas Mathematica, 102, 231–254.
12. Panda, G.K. (2009). Some fascinating properties of balancing numbers, In Proc. of Eleventh Internat. Conference on Fibonacci Numbers and Their Applications, Cong. Numerantium, 194, 185–189.
13. Panda, G. K., & Panda, A. K. (2015). Almost balancing numbers, Journal of the Indian Math. Soc., 82 (3–4), 147–156.
14. Panda, G. K., & Ray, P. K. (2005). Cobalancing numbers and cobalancers, Int. J. Math. Math. Sci., 8, 1189-1200.
15. Panda, G. K., & Ray, P. K. (2011). Some Links of Balancing and Cobalancing Numbers with Pell and Associated Pell Numbers, Bull. Inst. Math., Acad. Sin., 6 (1), 41–72.
16. Panda, A. K. (2017). Some Variants of the Balancing Sequences, Ph.D. thesis, National Institute of Technology Rourkela, India.
17. Ray, P. K. (2009). Balancing and Cobalancing Numbers, Ph.D. thesis, Department of Mathematics, National Institute of Technology, Rourkela, India.
18. Rout, S. S., & Panda, G. K. (2015). -gap balancing numbers, Period. Math. Hungar., 70 (1), 109–121.
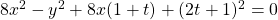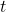19. Tekcan, A., Tayat, M., & Özbek, M. E. (2014). The Diophantine Equation and -Balancing Numbers, ISR Combinatorics, Article ID 897834.
20. Tekcan, A., Özkoç, A., & Özbek, M. E. (2016). Some Algebraic Relations on Integer Sequences Involving Oblong and Balancing Numbers, Ars Combinatoria, 128, 11–31.
21. Tekcan, A. (2019). Almost balancing, triangular and square triangular numbers, Notes on Number Theory and Discrete Maths., 25 (1), 108–121.