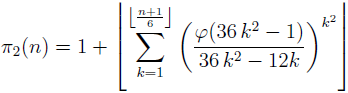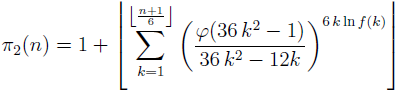Volume 19 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On the theorem of Conrey and Iwaniec
Original research paper. Pages 1–9
Jeffrey Stopple
Full paper (PDF, 177 Kb) | Abstract
An exposition on ‘Spacing of zeros of Hecke L-functions and the class number problem’ by Conrey and Iwaniec.
Method of infinite ascent applied on A3 ± nB2 = C3
Original research paper. Pages 10–14
Susil Kumar Jena
Full paper (PDF, 124 Kb) | Abstract
In this paper we will produce different formulae for which the Diophantine equation A3 ± nB2 = C3 will generate infinite number of co-prime integral solutions for (A, B, C) for any positive integer n.
Two-term Egyptian fractions
Original research paper. Pages 15–25
Tieling Chen and Reginald Koo
Full paper (PDF, 190 Kb) | Abstract
We study two-term Egyptian fraction representations of a given rational number. We consider the case of m/n where each prime factor p of n satisfies p ≡ ±1 (mod m): necessary and sufficient conditions for the existence of proper two-term Egyptian fraction expressions of such m/n are given, together with methods to find these representations. Furthermore, we determine the number of proper two-term Egyptian fraction expressions for 1/m, 2/m, 3/m, 4/m and 6/m.
Short remark on Möbius function
Original research paper. Pages 26–29
Krassimir T. Atanassov
Full paper (PDF, 119 Kb) | Abstract
Some representations of Möbius function μ are introduced, and illustrated with an example.
Extension of factorial concept to negative numbers
Original research paper. Pages 30–42
A. M. Ibrahim
Full paper (PDF, 125 Kb) | Abstract
This paper present a comparative study of the various types of positive factorial functions, among which include the conventional factorial, double factorial, quadruple factorial, superfactorial and hyperfactorial. Subsequently, an extension of the concepts of positive n! to negative numbers –n! is introduced. Based on this extension, a formulation of specific generalization cases for different forms of negative factorials are analyzed and presented.
Note on some explicit formulae for twin prime counting function
Original research paper. Pages 43–48
Mladen Vassilev-Missana
Full paper (PDF, 144 Kb) | Abstract
In the paper for any integer n ≥ 5 the validity of the formula
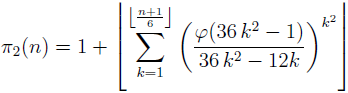
(where π
2 denotes the twin prime counting function and φ is Euler’s totient function) is established. Also for any integer n ≥ 5 the formula
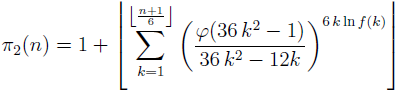
(where f is arbitrary artihmetic function with strictly positive values satisfying the condition
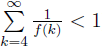
is proved.
Fibonacci and Lucas primes
Original research paper. Pages 49–59
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 132 Kb) | Abstract
The structures of Fibonacci numbers, Fn, formed when n equals a prime, p, are analysed using the modular ring Z5, Pascal’s Triangle as well as various properties of the Fibonacci numbers to calculate “Pascal-Fibonacci” numbers to test primality by demonstrating the many structural differences between the cases when Fn is prime or composite.
On the mean values of Dedekind sums over short intervals
Original research paper. Pages 60–68
Weixia Liu
Full paper (PDF, 167 Kb) | Abstract
The main purpose of this paper is using the mean values of Dirichlet L-functions and estimates for character sums to study the mean values of Dedekind sums over short intervals.
Generalization of a few results in integer partitions
Original research paper. Pages 69–76
Manosij Ghosh Dastidar and Sourav Sen Gupta
Full paper (PDF, 171 Kb) | Abstract
In this paper, we generalize a few important results in Integer Partitions; namely the results known as Stanley’s theorem and Elder’s theorem, and the congruence results proposed by Ramanujan for the partition function. We generalize the results of Stanley and Elder from a fixed integer to an array of subsequent integers, and propose an analogue of Ramanujan’s congruence relations for the ‘number of parts’ function instead of the partition function. We also deduce the generating function for the ‘number of parts’, use it to provide an alternative proof of Ramaunjan’s congruence relations, and relate the technical results with their graphical interpretations through a novel use of the Ferrer’s diagrams.
Note on Legendre symbols connecting with certain infinite series
Original research paper. Pages 77–83
Ramesh Kumar Muthumalai
Full paper (PDF, 143 Kb) | Abstract
Some applications of Legendre symbols connecting with certain infinite series are studied. In addition, some identities for Dirichlet series through Legendre symbols and Hurwitz zeta function are given.
Volume 19 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4