Segun Olofin Akerele and Olamide Esther Salami
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 1, Pages 82–90
DOI: 10.7546/nntdm.2025.31.1.82-90
Full paper (PDF, 265 Kb)
Details
Authors and affiliations
Segun Olofin Akerele ![]()
![]()
Department of Mathematics, University of Ibadan
Ibadan, Oyo-State, Nigeria
Olamide Esther Salami ![]()
![]()
Department of Mathematics, University of Ibadan
Ibadan, Oyo-State, Nigeria
Abstract
We find various series that involve the central binomial coefficients ![]() , harmonic numbers and Fibonacci numbers. Contrary to the traditional hypergeometric function
, harmonic numbers and Fibonacci numbers. Contrary to the traditional hypergeometric function ![]() approach, our method utilizes a straightforward transformation to obtain new evaluations linked to Fibonacci numbers and the golden ratio. We also gave a new series representation for
approach, our method utilizes a straightforward transformation to obtain new evaluations linked to Fibonacci numbers and the golden ratio. We also gave a new series representation for ![]() .
.
Keywords
- Central binomial coefficients
- Harmonic number
- Catalan number
- Fibonacci number
- Lucas number
2020 Mathematics Subject Classification
- 40A05
- 11B39
- 11B65
- 05A10
References
- Abramowitz, M., & Stegun, I. A. (1965). Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables (Vol. 55). Courier Corporation.
- Adegoke, K., Frontczak, R., & Goy, T. (2024). On some series involving the binomial coefficients
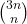 . Notes on Number Theory and Discrete Mathematics, 30(2), 319–334.
. Notes on Number Theory and Discrete Mathematics, 30(2), 319–334. - Bhandari, N. (2022). Binomial sums resulting to the ratio,
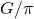 and
and 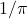 . Archimede Mathematical Journal, 9(1), 4–11.
. Archimede Mathematical Journal, 9(1), 4–11. - Chen, H. (2016). Interesting series Associated with Central Binomial Coefficients, Catalan Numbers and Harmonic Numbers. Journal of Integer Sequences, 19(1), Article 16.1.5.
- Chen, H. (2022). Interesting Ramanujan-like series associated with powers of central binomial coefficients. Journal of Integer Sequences, 25(1), Article 22.1.8.
- Graham, R. L., Knuth, D. E., & Patashnik, O. (1994). Concrete Mathematics. (2nd ed.). Addison-Wesley Publishing Company, Inc.
Manuscript history
- Received: 14 June 2024
- Revised: 2 April 2025
- Accepted: 7 April 2025
- Online First: 7 April 2025
Copyright information
![]() Ⓒ 2025 by the Authors.
Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Adegoke, K., Frontczak, R., & Goy, T. (2024). On some series involving the binomial coefficients
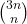 . Notes on Number Theory and Discrete Mathematics, 30(2), 319–334.
. Notes on Number Theory and Discrete Mathematics, 30(2), 319–334.
Cite this paper
Akerele, S. O., & Salami, O. E. (2025). Series associated with harmonic numbers, Fibonacci numbers and central binomial coefficients ![]() . Notes on Number Theory and Discrete Mathematics, 31(1), 82-90, DOI: 10.7546/nntdm.2025.31.1.82-90.
. Notes on Number Theory and Discrete Mathematics, 31(1), 82-90, DOI: 10.7546/nntdm.2025.31.1.82-90.


