Jovan Mikić
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 4, Pages 857–868
DOI: 10.7546/nntdm.2024.30.4.857-868
Full paper (PDF, 212 Kb)
Details
Authors and affiliations
Jovan Mikić ![]()
![]()
Faculty of Technology, Faculty of Natural Sciences and Mathematics, University of Banja Luka
Bosnia and Herzegovina
Abstract
The Gessel number ![]() is the number of lattice paths in the plane with
is the number of lattice paths in the plane with ![]() and
and ![]() steps from
steps from ![]() to
to ![]() that never touch any of the points from the set
that never touch any of the points from the set ![]() . We show that there is a close relationship between Gessel numbers
. We show that there is a close relationship between Gessel numbers ![]() and super Catalan numbers
and super Catalan numbers ![]() . A new class of binomial sums, so called
. A new class of binomial sums, so called ![]() sums, is used. By using one form of the Pfaff–Saalschütz theorem, a new recurrence relation for
sums, is used. By using one form of the Pfaff–Saalschütz theorem, a new recurrence relation for ![]() sums is proved. Finally, we prove that an alternating convolution of Gessel numbers
sums is proved. Finally, we prove that an alternating convolution of Gessel numbers ![]() multiplied by a power of a binomial coefficient is always divisible by
multiplied by a power of a binomial coefficient is always divisible by ![]() .
.
Keywords
- Gessel number
- Super Catalan number
- M sum
- Catalan number
- Pfaff–Saalschütz theorem
2020 Mathematics Subject Classification
- 05A10
- 11B65
References
- Allen, E., & Gheorghicius, I. (2014). A weighted interpretation for the super Catalan numbers. Journal of Integer Sequences, 17, Article 14.10.7.
- Calkin, N. J. (1998). Factors of sums of powers of binomial coefficients. Acta Arithmetica, 86, 17–26.
- Callan, D. (2005). A combinatorial interpretation for a super-Catalan recurrence. Journal of Integer Sequences, 8, Article 05.1.8
- Chen, X., & Wang, J. (2012). The super Catalan numbers
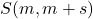 for
for 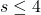 . Preprint. Available online at: https://arxiv.org/abs/1208.4196.
. Preprint. Available online at: https://arxiv.org/abs/1208.4196. - Chu, W., & Kilic¸, E. (2021). Binomial sums involving Catalan numbers. Rocky Mountain Journal of Mathematics, 4, 1221–1225.
- Gessel, I. M. (1992). Super ballot numbers. Journal of Symbolic Computation, 14, 179–194.
- Goulden, I. P. (1985). A bijective proof of the q-Saalschütz theorem. Discrete Mathematics, 57, 39–44.
- Graham, R. L., Knuth, D., & Patashnik, O. (1994). Concrete Mathematics (2nd ed.). Addison-Wesley.
- Guo, V. J. W. (2018). A new proof of the q-Dixon identity. Czechoslovak Mathematical Journal, 68, 577–580.
- Guo, V. J. W., Jouhet, F., & Zeng, J. (2007). Factors of alternating sums of products of binomial and q-binomial coefficients. Acta Arithmetica, 127, 17–31.
- Guo, V. J. W. (2014). Proof of two divisibility properties of binomial coefficients conjectured by Z. W. Sun. Electronic Journal of Combinatorics, 21, # P54.
- Killpatrick, K. (2023). Super FiboCatalan numbers and generalized FiboCatalan numbers. Preprint. Available online at: https://www.researchgate.net/publication/373437785.
- Knuth, D. E. (1968). The Art of Computer Programming, Vol. 1 (3rd ed.). Addison-Wesley.
- Koshy, T. (2009). Catalan Numbers with Applications. Oxford University Press.
- Mikić, J. (2018). A method for examining divisibility properties of some binomial sums. Journal of Integer Sequences, 21, Article 18.8.7.
- Mikić, J. (2014). A note on the Gessel numbers. JP Journal of Algebra, Number Theory and Applications, 63, 225–235.
- Mikić, J. (2020). New class of binomial sums and their applications. Proceedings of 3rd Croatian Combinatorial Days, September 21-22, 2020, Zagreb. Available online at: https://www.grad.hr/crocodays/proc_ccd3/mikic_final.pdf.
- Mikić, J. (2021, March 15). On a new alternating convolution formula for the Super Catalan numbers. Romanian Mathematical Magazine. Available online at: https://www.ssmrmh.ro/2021/03/15/on-an-alternative-convolution-formula-for-the-catalan-super-numbers/
- Mikić, J. (2020). On a certain sums divisible by the central binomial coefficient. Journal of Integer Sequences, 23, Article 20.1.6.
- Mikić, J. (2019). Two new identities involving the Catalan numbers and sign-reversing involutions. Journal of Integer Sequences, 22, Article 19.7.7.
- Pfaff, J. (1797). Observationes analyticae ad L. Euler Institutiones Calculi Integralis, Vol. IV, Supplem. II et IV, Historia de 1793, Nova Acta Academiae Scientiarum Imperialis Petropolitanae, 11 (1797), 38–57.
- Pippenger, N., & Schleich, K. (2006). Topological characteristics of random triangulated surfaces. Random Structures and Algorithms, 28, 247–288.
- Prodinger, H. (2019). Two new identities involving the Catalan numbers: A classical approach. Preprint. Available online at: https://arxiv.org/abs/1911.07604.
- Schaeffer, G. (2003). A combinatorial interpretation of super-Catalan numbers of order two. Manuscript.
- Slater, L. J. (1966). Generalized Hypergeometric Functions. Cambridge University Press, Cambridge.
- Stanley, R. P. (2009). Bijective proof problems. Available online at: https://math.mit.edu/~rstan/bij.pdf
Manuscript history
- Received: 3 July 2024
- Revised: 3 December 2024
- Accepted: 11 December 2024
- Online First: 16 December 2024
Copyright information
![]() Ⓒ 2024 by the Author.
Ⓒ 2024 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Mikić, J. (2025). On a new congruence in the Catalan triangle. Notes on Number Theory and Discrete Mathematics, 31(3), 667-682.
Cite this paper
Mikić, J. (2024). Factors of alternating convolution of the Gessel numbers. Notes on Number Theory and Discrete Mathematics, 30(4), 857-868, DOI: 10.7546/nntdm.2024.30.4.857-868.


