Anuraag Saxena and Abhimanyu Kumar
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 3, Pages 602–612
DOI: 10.7546/nntdm.2024.30.3.602-612
Full paper (PDF, 645 Kb)
Details
Authors and affiliations
Anuraag Saxena ![]()
Department of Electronics and Communication Engineering,
Thapar Institute of Engineering and Technology
Patiala, Punjab 147004, India
Abhimanyu Kumar ![]()
![]()
Department of Electrical and Instrumentation Engineering,
Thapar Institute of Engineering and Technology
Patiala, Punjab 147004, India
Abstract
The degree of insulation of a prime ![]() is defined as the largest interval around
is defined as the largest interval around ![]() within which no other prime exists. A prime
within which no other prime exists. A prime ![]() is classified as insulated if its degree of insulation is greater than that of its neighbouring primes. This leads to the emergence of a new sequence, known as the insulated primes, which starts with 7, 13, 23, 37, 53, 67, 89, 103, 113, 131, 139, 157, 173, 181, 193, 211, 233, 277, 293, and so on. This paper explores several properties and intriguing relationships concerning the degree of insulation, and includes a brief heuristic study of the insulated primes. Finally, the reader is left with a captivating open problem.
is classified as insulated if its degree of insulation is greater than that of its neighbouring primes. This leads to the emergence of a new sequence, known as the insulated primes, which starts with 7, 13, 23, 37, 53, 67, 89, 103, 113, 131, 139, 157, 173, 181, 193, 211, 233, 277, 293, and so on. This paper explores several properties and intriguing relationships concerning the degree of insulation, and includes a brief heuristic study of the insulated primes. Finally, the reader is left with a captivating open problem.
Keywords
- Special prime sequences
- Prime gaps
2020 Mathematics Subject Classification
- 11A41
- 11K31
References
- Alweiss, R., & Luo, S. (2018). Bounded gaps between primes in short intervals. Research in Number Theory, 4, Article 15.
- Baker, R. C., Harman, G. & Pintz, J. (2001). The difference between consecutive primes, II. Proceedings of the London Mathematical Society, 83(3), 532–562.
- Carneiro, E., Milinovich, M. B., & Soundararajan, K. (2019). Fourier optimization and prime gaps. Commentarii Mathematici Helvetici, 94, 533–568.
- Dudek, A. W. (2015). On the Riemann hypothesis and the difference between primes. International Journal of Number Theory, 11, 771–778.
- Dudek, A. W., Grenié, L., & Molteni, G. (2016). Primes in explicit short intervals on RH. International Journal of Number Theory, 12, 1391–1407.
- Dusart, P. (1999). The kth prime is greater than
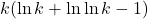 for
for 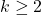 . Mathematics of Computation, 68(225), 411–415.
. Mathematics of Computation, 68(225), 411–415. - Guy, R. K. (2004). Unsolved Problems in Number Theory. Springer Verlag, New York.
- Heath-Brown, D. R., & Iwaniec, H. (1979). On the difference between consecutive primes. Inventiones Mathematicae, 55(1), 49–69.
- Heath-Brown, D. R (1988). The number of primes in a short interval. Journal fur die reine ¨ und angewandte Mathematik, 389, 22–63.
- Hoheisel, G. (1930). Primzahlprobleme in der Analysis. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, 33, 3–11.
- Heilbronn, H. A. (1933). Über den Primzahlsatz von Herrn Hoheisel. Mathematische Zeitschrift, 36(1), 394–423.
- Huxley, M. N. (1972). On the difference between consecutive primes. Inventiones
Mathematicae, 15(2), 164–170. - Ingham, A. E. (1937). On the difference between consecutive primes. The Quarterly Journal of Mathematics, 8(1), 255–266.
- Kumar, A. (2022). Prime floor and prime ceiling functions. Integers, 22, #A41.
- Maynard, J. (2015). Small gaps between primes. Annals of Mathematics, 181, 383–413.
- Polymath, D. H. J. (2014). Variants of the Selberg sieve, and bounded intervals containing many primes. Research in the Mathematical Sciences, 1, Article ID 12.
- Ramaré, O., & Saouter, Y. (2003). Short effective intervals containing primes. Journal of Number Theory, 98, 10–33.
- Rosser, B. (1941). Explicit bounds for some functions of prime numbers. American Journal of Mathematics, 63(1), 211–232.
- Tchudakoff, N. G. (1936). On the difference between two neighboring prime numbers. Matematicheskii Sbornik, 1, 799–814.
- Wolf, M. (2011). Some heuristics on the gaps between consecutive primes. Preprint arXiv:1102.0481.
- Zhang, Y. (2014). Bounded gaps between primes. Annals of Mathematics, 179(3), 1121–1174.
Manuscript history
- Received: 23 June 2023
- Revised: 27 May 2024
- Accepted: 1 October 2024
- Online First: 24 October 2024
Copyright information
![]() Ⓒ 2024 by the Authors.
Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Saxena, A., & Kumar, A. (2024). Insulated primes. Notes on Number Theory and Discrete Mathematics, 30(3), 602-612, DOI: 10.7546/nntdm.2024.30.3.602-612


