Brenda Navarro-Flores, José M. González-Barrios and Raúl Rueda
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 4, Pages 724–736
DOI: 10.7546/nntdm.2023.29.4.724-736
Full paper (PDF, 257 Kb)
Details
Authors and affiliations
Brenda Navarro-Flores ![]()
Department of Probability and Statistics, IIMAS,
Universidad Nacional Autónoma de México, Mexico City, Mexico
José M. González-Barrios ![]()
![]()
Department of Probability and Statistics, IIMAS,
Universidad Nacional Autónoma de México, Mexico City, Mexico
Raúl Rueda ![]()
![]()
Department of Probability and Statistics, IIMAS,
Universidad Nacional Autónoma de México, Mexico City, Mexico
Abstract
Prime numbers have been always of great interest. In this work, we explore the prime numbers from a sieve other than the Eratosthenes sieve. Given a prime number ![]() , we consider the binary expansion of
, we consider the binary expansion of ![]() and, in particular, the size of the period of
and, in particular, the size of the period of ![]() . We show some results that relate the size of the period to properties of the prime numbers.
. We show some results that relate the size of the period to properties of the prime numbers.
Keywords
- Prime numbers
- Order induced by binary expansions
- New sieve
2020 Mathematics Subject Classification
- 11A41
- 11B83
References
- Andrica, D. (1986). Note on a conjecture in prime number theory. Studia Universitatis Babeș-Bolyai Mathematica, 31, 44–48.
- Artin, E. (1965). The Collected Papers of Emil Artin. Addison-Wesley. Mathematical Reviews, 31, #1159.
- Ash, R. B. (1972). Real Analysis and Probability. Academic Press, New York.
- Bang, A. S. (1886). Taltheoretiske Undersøgelser. Tidsskrift for Mathematik. FEMTE RÆKKE, 4, 70–80.
- Bang, A. S. (1886). Taltheoretiske Undersøgelser (continued). Tidsskrift for Mathematik. FEMTE RÆKKE, 4, 130–137.
- Birkhoff, G. D., & Vandiver, H. S. (1904). On the integral divisors of
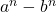 . Annals of Mathematics, 5, 173–180.
. Annals of Mathematics, 5, 173–180. - Burton, D. M. (2011). The History of Mathematics: An Introduction (7th ed.). McGraw-Hill, New York.
- Caldwell, C., & Dubner, H. (1998). Unique-period primes. Journal of Recreational Mathematics, 29(1), 43–48.
- Conway, H. J., & Guy, R. K. (1995). The Book of Numbers. Copernicus, Springer-Verlag, New York.
- Gauss, C. F. (1863). Werke, Vol. 2 (1st ed.), Göttingen: Teubner, 444–447.
- Hardy, G. H., & Wright, E. M. (2008). An Introduction to the Theory of Numbers, (6th ed.). Oxford University Press, Oxford.
- Hoffman, P. (1998). The Man Who Loved Only Numbers (1st ed.). Hyperion Books, New York.
- Hooley, C. (1967). On Artin’s conjecture. Journal für die reine und angewandte Mathematik, 225, 209–220.
- Koshy, T. (2002). Elementary Number Theory with Applications. Harcourt/Academic Press, San Diego.
- Meijer, A. R. (1995). The binary expansion of
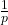 . The American Mathematical Monthly, 102(5), 427–430.
. The American Mathematical Monthly, 102(5), 427–430. - Midy, E. (1836). De Quelques Propriétés des Nombres et des Fractions Decimales Périodiques. Nantes, France.
- OEIS Foundation Inc. (2022). Entry A108974. The On-Line Encyclopedia of Integer Sequences. Available online at: https://oeis.org/A108974.
- Oppermann, L. (1882). Om vor Kundskab om Primtallenes Mængde mellem givne Grændser. Oversigt over det Kongelige Danske Videnskabernes Selskabs Forhandlinger og dets Medlemmers Arbejder, 169–179.
- Ribenboim, P. (1988). The Book of Prime Number Records (1st ed.). Springer-Verlag, New York.
- Ribenboim, P. (1996). The New Book of Prime Number Records. (1st. ed.). Springer, New York.
- Rosen, K. H. (1992). Elementary Number Theory and its Applications (6th ed.).
Addison-Wesley, Reading, MA. - Rosser, J. B. (1938). The n-th prime is greater than
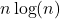 . Proceedings of The London Mathematical Society, 45, 21–44.
. Proceedings of The London Mathematical Society, 45, 21–44. - Rotman, J. (2005). A First Course in Abstract Algebra. Prentice Hall, New Jersey.
- Silvester, J. R. (1999). Decimal déjà vu. The Mathematical Gazette, 83(498), 453–463.
- Tripathi, A. (2012). A curious property of the decimal expansion of reciprocals of primes. The Pi Mu Epsilon Journal, 13(7), 427–430.
- Weisstein, E. W. “Primitive Prime Factor.” MathWorld – A Wolfram Web Resource. Available online at: https://mathworld.wolfram.com/PrimitivePrimeFactor.html
- Yates, S. (1980). Periods of unique primes. Mathematics Magazine, 53(5), 314–314.
- Zsigmondy, K. (1892). Zur Theorie der Potenzreste. Journal Monatshefte für Mathematik, 3(1), 265–284
Manuscript history
- Received: 10 November 2022
- Revised: 27 July 2023
- Accepted: 13 November 2023
- Online First: 21 November 2023
Copyright information
![]() Ⓒ 2023 by the Authors.
Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Navarro-Flores, B., González-Barrios, J. M., & Rueda, R. (2023). Binary expansions of prime reciprocals. Notes on Number Theory and Discrete Mathematics, 29(4), 724-736, DOI: 10.7546/nntdm.2023.29.4.724-736.


