Gabriel Guedes and Ricardo Machado
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 4, Pages 705–712
DOI: 10.7546/nntdm.2023.29.4.705-712
Full paper (PDF, 302 Kb)
Details
Authors and affiliations
Gabriel Guedes ![]()
![]()
Department of Mathematics, Rural Federal University of Pernambuco (UFRPE)
Recife-PE, Brazil
Ricardo Machado ![]()
![]()
Department of Mathematics, Rural Federal University of Pernambuco (UFRPE)
Recife-PE, Brazil
Abstract
In this article we focus on the solutions of a congruence equation: ![]() . Using the main result of this article and the SageMath software, we improve largely the number of known solutions. Furthermore, we prove that some famous numbers like even perfect numbers and Wieferich primes are connected to solutions of this equation.
. Using the main result of this article and the SageMath software, we improve largely the number of known solutions. Furthermore, we prove that some famous numbers like even perfect numbers and Wieferich primes are connected to solutions of this equation.
Keywords
- Perfect numbers
- Wieferich primes
- Binomial coefficient
- Algorithmic number theory
- Wolstenholme converse problem
2020 Mathematics Subject Classification
- 11A07
- 11A41
- 11B65
- 11B75
- 11-04.
References
- Chuan-Chong, C., & Khee-Meng, K. (1992). Principles and Techniques in Combinatorics. World Scientific, Singapore.
- Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms. (3rd ed.). MIT Press, Cambridge, Massachusetts.
- Granville, A. (2020). Number Theory Revealed: A Masterclass. American Mathematical Society, Providence, Rhode Island.
- Guy, R. (2004). Unsolved Problems in Number Theory. Springer Science + Business Media, New York.
- McIntosh, R. J. (1995). On the converse of Wolstenholme’s theorem. Acta Arithmetica, 71(4), 381–389.
- Mersenne.org (2023). List of known Mersenne prime numbers. Available online at: https://www.mersenne.org/primes/ .
- OEIS Foundation Inc. (2023). Composite integers n such that binomial
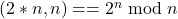 . Entry A084699. The On-Line Encyclopedia of Integer Sequences. Available online at: https://oeis.org/A084699 .
. Entry A084699. The On-Line Encyclopedia of Integer Sequences. Available online at: https://oeis.org/A084699 . - Ribenboim, P. (2004). The Little Book of Bigger Primes. (Vol. 811). Springer, New York.
Manuscript history
- Received: 4 April 2023
- Revised: 22 August 2023
- Accepted: 25 October 2023
- Online First: 16 November 2023
Copyright information
![]() Ⓒ 2023 by the Authors.
Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Guedes, G., & Machado, R. (2023). Perfect numbers, Wieferich primes and the solutions of ![]() . Notes on Number Theory and Discrete Mathematics, 29(4), 705-712, DOI: 10.7546/nntdm.2023.29.4.705-712.
. Notes on Number Theory and Discrete Mathematics, 29(4), 705-712, DOI: 10.7546/nntdm.2023.29.4.705-712.


