New approaches of (q,k)-Fibonacci–Pell sequences via linear difference equations. Applications

Irene Magalhães Craveiro, Elen Viviani Pereira Spreafico and Mustapha Rachidi
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 4, Pages 647–669
DOI: 10.7546/nntdm.2023.29.4.647-669
Full paper (PDF, 317 Kb)

Details

Authors and affiliations

Irene Magalhães Craveiro
Mathematics Department, Universidade Federal da Grande Dourados
Dourados-MS, Brazil

Elen Viviani Pereira Spreafico
Institute of Mathematics, Universidade Federal de Mato Grosso do Sul
Campo Grande-MS, Brazil

Mustapha Rachidi
Institute of Mathematics, Universidade Federal de Mato Grosso do Sul
Campo Grande-MS, Brazil

Abstract

In this paper we establish some explicit formulas of (q,k)-Fibonacci–Pell sequences via linear difference equations of order 2 with variable coefficients, and explore some of their new properties. More precisely, our results are based on two approaches, namely, the determinantal and the nested sums approaches, and their closed relations. As applications, we investigate the q-analogue Cassini identities and examine a pair of Rogers–Ramanujan type identities.

Keywords

• (q, k)-Fibonacci sequence
• (q, k)-Pell sequence
• Recursive sequences of variable coefficients
• Tridiagonal matrix
• Nested sums
• (q, k)-Cassini identities
• Rogers–Ramanujan identities

2020 Mathematics Subject Classification

• 65Q30
• 65Q30
• 11C20

References

1. Abderraman Marrero, J., & Rachidi, M. (2012). Application of the companion factorization to linear non-autonomous area-preserving maps. Linear and Multilinear Algebra, 60(2), 201–217.
2. Abderraman Marrero, J., & Rachidi, M. (2013). A note on representations for the inverses of tridiagonal matrices. Linear and Multilinear Algebra, 61(9), 1181-119.
3. Abderraman Marrero, J., & Rachidi, M. (2011). Companion factorization in the general linear group 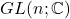and applications. Linear Algebra and its Applications, 434, 1261–1271.
4. Andrews, G. E. (1986). q-Series: Their development and application in analysis, number theory, combinatorics, physics an computer algebra. CBMS Regional Conference Series in Mathematics, American Mathematical Society, Providence, RI, 66, 87–93.
5. Baruah, N. D., & Bora, J. (2007). Further analogues of the Rogers–Ramanujan functions with applications to partitions. Integers: Electronic Journal of Combinatorial Number Theory, 7(2), Article ID #A05, 22 pages.
6. Benkhaldoun, H., Ben Taher, R., & Rachidi, M. (2021). Periodic matrix difference equations and companion matrices in blocks: Some applications. Arabian Journal of Mathematics, 10, 555–574.
7. Ben Taher, R., Benkhaldoun, H., & Rachidi, M. (2016). On some class of periodic-discrete homogeneous difference equations via Fibonacci sequences. Journal of Difference Equations and Applications, 22(9), 1292–1306.
8. Briggs, K. S., Little, D. P., & Sellers, J. A. (2010). Combinatorial proofs of various q-Pell identities via tilings. Annals of Combinatorics, 14(4), 407–418.
9. Craveiro, I. M. (2004). Extensões e Interpretações Combinatórias para os Números de Fibonacci, Pell e Jacobsthal. 16/02/2004. 116fl. Tese. UNICAMP. Campinas, SP.
10. Craveiro, I. M., Pereira Spreafico, E. V., & Rachidi, M. (2023). Generalized Cassini identities via the generalized Fibonacci fundamental system. Applications. Indian Journal of Pure and Applied Mathematics, DOI: 10.1007/s13226-023-00430-1.
11. Ercolano, J. (1979). Matrix generators of Pell sequences. The Fibonacci Quarterly, 17(1), 71–77.
12. Kittappa, R. K. (1993). A representation of the solution of the nth order linear difference equation with variable coefficients. Linear Algebra and its Applications, 193, 211–222.
13. MacMahon, A. P. (1918). Combinatory Analysis, Volume 2. Cambridge University Press, London.
14. Mallik, R. K. (2001). The inverse of a tridiagonal matrix. Linear Algebra and its
    Applications, 325, 109–139.
15. Mallik, R. K. (1997). On the solution of a second order linear homogeneous difference equation with variable coefficients. Journal of Mathematical Analysis and Applications, 215, 32–47.
16. Mallik, R. K. (1998). Solutions of linear difference equations with variable coefficients. Journal of Mathematical Analysis and Applications, 222, 79–91.
17. Mansour, T., & Shattuck, M. (2011). Restricted partitions and q-Pell numbers. Open Mathematics, 9(2), 346–355.
18. Pan, H. (2006). Arithmetic properties of q-Fibonacci numbers and q-Pell numbers. Discrete Mathematics, 306, 2118–2127.
19. Pereira Spreafico, E. V., & Rachidi, M. (2019). Fibonacci fundamental system and
    generalized Cassini identity. The Fibonacci Quarterly, 57(2), 155–157.
20. Popenda, J. (1987). On expression for the solutions of the second order difference equations. Proceedings of the American Mathematical Society, 100(1), 87–93.
21. Santos, J. P. O. (1991). Computer Algebra and Identities of the Rogers–Ramanujan Type. Ph.D. Thesis, Pennsylvania State University, United States.
22. Santos, J. P. O., & Sills, A. V. (2002). q-Pell sequences and two identities of V. A. Lebesgue. Discrete Mathematics, 257(1), 125–142.
23. Shannon, A. G., & Horadam, A. F. (2004). Generalized Pell numbers and polynomials. In: Howard. F. T. (Ed.). Applications of Fibonacci Numbers. Springer, Dordrecht.
24. Slater, L. J. (1952). Further identities of the Rogers–Ramanujan Type. Proceedings of the London Mathematical Society, 2(1), 157–167.

Manuscript history

• Received: 14 March 2023
• Revised: 21 September 2023
• Accepted: 4 October 2023
• Online First: 11 October 2023

Copyright information

Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).