József Sándor
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 3, Pages 454–461
DOI: 10.7546/nntdm.2023.29.3.454-461
Full paper (PDF, 259 Kb)
Details
Authors and affiliations
József Sándor ![]()
![]()
Department of Mathematics, Babeș-Bolyai University
Cluj-Napoca, Romania
Abstract
As a continuation of [10] and [11], we offer some new inequalities for the prime counting function ![]() Particularly, a multiplicative analogue of the Hardy–Littlewood conjecture is provided. Improvements of the converse of Landau’s inequality are given. Some results on
Particularly, a multiplicative analogue of the Hardy–Littlewood conjecture is provided. Improvements of the converse of Landau’s inequality are given. Some results on ![]() are offered,
are offered, ![]() denoting the
denoting the ![]() -th prime number. Results on
-th prime number. Results on ![]() are also considered.
are also considered.
Keywords
- Prime counting function
- Inequalities
- Hardy–Littlewood conjecture
- Landau’s inequality
- Prime numbers
2020 Mathematics Subject Classification
- 11A25
- 11A41
References
- Alzer, H., & Kwong, M. K. (2022). On Landau’s inequality for the prime counting function. Journal of Integer Sequences, 25, Article 22.7.3.
- Alzer, H., Kwong, M. K., & Sándor, J. (2022). Inequalities involving
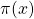 . Rendiconti del Seminario Matematico della Università di Padova, 147(1), 237–251.
. Rendiconti del Seminario Matematico della Università di Padova, 147(1), 237–251. - Dusart, P. (1999). Inégalités explicit pour
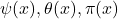 et les nombres premiers. Comptes rendus mathématiques de l’Académie des sciences. La Société Royale du Canada, 21(2), 53–59.
et les nombres premiers. Comptes rendus mathématiques de l’Académie des sciences. La Société Royale du Canada, 21(2), 53–59. - Miliakos, G. (2022). Open Questions OQ 5762 and OQ 5760. Octogon Mathematical Magazine, 30(2), 1510.
- Panaitopol, L. (1998). On the inequality
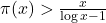 . Analele Universităţii din Bucureşti, Seria Matematica. XLVII(2), 187–192.
. Analele Universităţii din Bucureşti, Seria Matematica. XLVII(2), 187–192. - Panaitopol, L. (1998). On the inequality
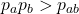 . Bulletin Mathématique de la Société des Sciences Mathématiques de Roumanie, 41(89), No. 2, 135–139.
. Bulletin Mathématique de la Société des Sciences Mathématiques de Roumanie, 41(89), No. 2, 135–139. - Ribenboim, P. (1996). The New Book of Prime Number Records. Springer.
- Rosser, J. B., & Schoenfeld, L. (1962). Approximate formulas for some functions of prime numbers. Illinois Journal of Mathematics, 6, 64–94.
- Sándor, J. (2006). On some inequalities of Dusart and Panaitopol on the function π(x). Octogon Mathematical Magazine, 14 (2), 592–594.
- Sándor, J. (2021). On certain inequalities for the prime counting function. Notes on Number Theory and Discrete Mathematics, 27(4), 149–153.
- Sándor, J. (2022). On certain inequalities for the prime counting function – Part II. Notes on Number Theory and Discrete Mathematics, 28(1), 124–128.
- Sándor, J., Mitrinović, D. S., & Cristici, B. (2005). Handbook of Number Theory I, Springer.
Manuscript history
- Received: 5 May 2023
- Revised: 21 June 2023
- Accepted: 30 June 2023
- Online First: 3 July 2023
Copyright information
![]() Ⓒ 2023 by the Author.
Ⓒ 2023 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Sándor, J. (2023). On certain inequalities for the prime counting function – Part III. Notes on Number Theory and Discrete Mathematics, 29(3), 454-461, DOI: 10.7546/nntdm.2023.29.3.454-461.


