Mustafa Ismail, Salah Eddine Rihane and M. Anwar
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 3, Pages 462–473
DOI: 10.7546/nntdm.2023.29.3.462-473
Full paper (PDF, 202 Kb)
Details
Authors and affiliations
Mustafa Ismail ![]()
![]()
Department of Mathematics, Faculty of Science,
University of Ain Shams, Egypt
Salah Eddine Rihane ![]()
![]()
Department of Mathematics, Institute of Science and Technology,
University Center of Mila, Algeria
M. Anwar ![]()
![]()
![]()
Department of Mathematics, Faculty of Science,
University of Ain Shams, Egypt
Abstract
Let ![]() be the Narayana sequence defined by the recurrence
be the Narayana sequence defined by the recurrence ![]() for all
for all ![]() with intital values
with intital values ![]() and
and ![]() . In this paper, we fully characterize the
. In this paper, we fully characterize the ![]() -adic valuation of
-adic valuation of ![]() and
and ![]() and then we find all positive integer solutions
and then we find all positive integer solutions ![]() to the Brocard–Ramanujan equation
to the Brocard–Ramanujan equation ![]() where
where ![]() is a Narayana number.
is a Narayana number.
Keywords
- Narayana sequence
- Factorials
- p-adic valuation
2020 Mathematics Subject Classification
- 11B39
- 11D72
References
- Allouche, J. P., & Johnson, T. (1996). Narayana’s cows and delayed morphisms. Journées d’Informatique Musicale, ˆıle de Tatihou, France. Available online at: https://hal.science/hal-02986050
- Berndt, B. C., & Galway, W. F. (2000). On the Brocard–Ramanujan Diophantine equation
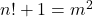 . The Ramanujan Journal, 4(2), 41–42.
. The Ramanujan Journal, 4(2), 41–42. - Bilgici, G. (2016). The generalized order-k Narayana’s cows numbers. Mathematica Slovaca, 66(4), 795–802.
- Brocard, H. (1876). Question 166, Nouv. Corresp. Math., 2, 287.
- Facó, V., & Marques, D. (2016). Tribonacci numbers and the Brocard–Ramanujan equation. Journal of Integer Sequences, 19(4), 4–16.
- Grossman, G., & Luca, F. (2002). Sums of factorials in binary recurrence sequences. Journal of Number Theory, 93(2), 87–107.
- Luca, F. (1999). Products of factorials in binary recurrence sequences. The Rocky Mountain Journal of Mathematics, 29(4), 1387–1411.
- Luca, F., & Stanica, P. (2006).
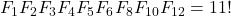 . Portugaliae Mathematica, 63(3), 251–260.
. Portugaliae Mathematica, 63(3), 251–260. - Marques, D. (2012). Fibonacci numbers at most one away from the product of factorials. Notes on Number Theory and Discrete Mathematics, 18(3), 13–19.
- Marques, D. (2012). The order of appearance of product of consecutive Fibonacci numbers. Fibonacci Quarterly, 50(2), 132–139.
- Overholt, M. (1993). The Diophantine equation
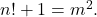 Bulletin of the London Mathematical Society, 25(2), 104.
Bulletin of the London Mathematical Society, 25(2), 104. - Ramanujan, S. (1962). Ramanujan’s Collected Works. Chelsea, New York.
- Zhou, C. (1999). Constructing identities involving Kth-order F-L numbers by using the characteristic polynomial. Applications of Fibonacci Numbers, 369–379.
Manuscript history
- Received: 20 July 2022
- Revised: 25 April 2023
- Accepted: 27 June 2023
- Online First: 6 July 2023
Copyright information
![]() Ⓒ 2023 by the Authors.
Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Marques, D. (2012). Fibonacci numbers at most one away from the product of factorials. Notes on Number Theory and Discrete Mathematics, 18(3), 13–19.
Cite this paper
Ismail, M., Rihane, S. E., Anwar, M. (2023). Narayana sequence and the Brocard–Ramanujan equation. Notes on Number Theory and Discrete Mathematics, 29(3), 462-473, DOI: 10.7546/nntdm.2023.29.3.462-473.


