Mladen Vassilev-Missana
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 19, 2013, Number 3, Pages 24–27
Full paper (PDF, 148 Kb)
Details
Authors and affiliations
Mladen Vassilev-Missana ![]()
5 V. Hugo Str., 1124 Sofia, Bulgaria
Abstract
In the paper the new formulae for the prime counting function π:
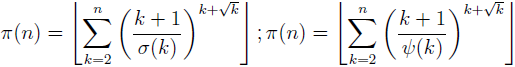
(where σ is the sum-of-divisor function and ψ is the Dedekind’s function) are proposed and proved. Also a general theorem (Theorem 1) is obtained that gives infinitely many explicit formulae for the prime counting function π (depending on arbitrary arithmetic function with strictly positive values, satisfying certain condition).
Keywords
- Prime number
- Composite number
- Arithmetic function
AMS Classification
- 11A25
- 11A41
References
- Atanassov, K. T. Remark on Jacobsthal numbers, Part 2. Notes on Number Theory and Discrete Mathematics, Vol. 17, 2011, No. 2, 37–39.
- Atanassov, K. T. Short remarks on Jacobsthal numbers. Notes on Number Theory and Discrete Mathematics, Vol. 18, 2012, No. 2, 63–64.
- Rabago, J. F. T. Circulant Determinant Sequence with Binomial Coefficients, Scientia Magna (on review).
- Shang, Y. On the modifications of the Pell–Jacobsthal numbers, Scientia Magna, Vol. 8, 2012, No. 3, 68–70.
Related papers
- Shannon, A. G. & Leyendekkers, J. V. (2017). On Legendre’s Conjecture. Notes on Number Theory and Discrete Mathematics, 23(2), 117-125.
Cite this paper
Vassilev-Missana, M. (2013). New explicit representations for the prime counting function. Notes on Number Theory and Discrete Mathematics, 19(3), 24-27.


