On q-generalized hyperharmonic numbers with two parameters

Neşe Ömür, Sibel Koparal and Ömer Duran
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 4, Pages 884–898
DOI: 10.7546/nntdm.2025.31.4.884-898
Full paper (PDF, 728 Kb)

Details

Authors and affiliations

Neşe Ömür
Department of Mathematics, Faculty of Science and Arts, Kocaeli University, Türkiye

Sibel Koparal
Department of Mathematics, Faculty of Science and Arts, Bursa Uludağ University, Türkiye

Ömer Duran
Department of Mathematics, Faculty of Science and Arts, Kocaeli University, Türkiye

Abstract

In this paper, we introduce q-generalized harmonic numbers with two parameters \omega and \xi , H_{\mu,\lambda,q}(\omega ,\xi ) for integers \mu,\lambda such that \lambda\geq \mu. With the help of these numbers, we define a new family of numbers which is called q-generalized hyperharmonic numbers with two parameters \omega and \xi of order r, H_{\mu,\lambda,q}^{r}(\omega,\xi ) for integer r. Then, we consider special matrices whose entries are given by these numbers and give some matrix multiplications. Additionally, we derive some combinatorial identities for H_{\mu,\lambda,q}(\omega ,\xi ) and H_{\mu,\lambda,q}^{r}(\omega ,\xi ) by matrix methods.

Keywords

  • Matrices
  • q-analogue
  • Harmonic numbers
  • Generalized harmonic numbers

2020 Mathematics Subject Classification

  • 11C20
  • 11B65

References

  1. Bahşi, M., & Solak, S. (2013). An application of hyperharmonic numbers in matrices. Hacettepe Journal of Mathematics and Statistics, 42(4), 387–393.
  2. Benjamin, A., Gaebler, D., & Gaebler, R. (2003). A combinatorial approach to hyperharmonic numbers. Integers, 3, Article ID #A15.
  3. Boyadzhiev, K. N. (2009). Harmonic number identities via Euler’s transform. Journal of Integer Sequences, 12(6), Article ID 09.6.1.
  4. Cereceda, J. L. (2015). An introduction to hyperharmonic numbers. International Journal of Mathematical Education in Science and Technology, 46(3), 461–469.
  5. Cheon, G. S., & El-Mikkawy, M. E. A. (2007). Generalized harmonic number identities and a related matrix representation. Journal of the Korean Mathematical Society, 44(2), 487–498.
  6. Cheon, G. S., & El-Mikkawy, M. E. A. (2008). Generalized harmonic numbers with Riordan arrays. Journal of Number Theory, 128(2), 413–425.
  7. Duran, Ö., Ömür, N., & Koparal, S. (2025). Double 3-dimensional Riordan arrays and their applications. Boletim da Sociedade Paranaense de Matematica, 43, DOI: 10.5269/bspm.66598 (15 pages).
  8. Frontczak, R. (2020). Harmonic sums via Euler’s transform: Complementing the approach of Boyadzhiev. Journal of Integer Sequences, 23, Article ID 20.3.2.
  9. Furman, E. (2007). On the convolution of the negative binomial random variables. Statistics and Probability Letters, 77(2), 169–172.
  10. Genčev, M. (2011). Binomial sums involving harmonic numbers. Mathematica Slovaca, 61(2), 215–226.
  11. Graham, R. L., Knuth, D. E., & Patashnik, O. (1994). Concrete Mathematics: A Foundation for Computer Science. Addison Wesley Publishing Co.
  12. Guo, D., & Chu, W. (2021). Summation formulae involving multiple harmonic numbers. Applicable Analysis and Discrete Mathematics, 15(1), 201–212.
  13. Kim, D. S., & Kim, T. (2013). Identities involving harmonic and hyperharmonic numbers. Advances in Difference Equations, 2013(1), Article ID 235.
  14. Kızılateş, C., & Tuğlu, N. (2015). Some combinatorial identities of q-harmonic and q-hyperharmonic numbers. Communications in Mathematics and Applications, 6(2), 33–40.
  15. Koparal, S., & Duran, Ö., & Ömür, N. (2021). On identities involving generalized harmonic, hyperharmonic and special numbers with Riordan arrays. Special Matrices, 9(1), 22–30.
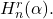  16. Koparal, S., Ömür, N., & Çolak, C. D. (2020). Some applications on q-analog of the generalized hyperharmonic numbers of order r,H_{n}^{r} (\alpha ). Hacettepe Journal of Mathematics and Statistics, 49(6), 2094–2103.
  17. Li, R. (2021). Euler sums of generalized alternating hyperharmonic numbers. Rocky Mountain Journal of Mathematics, 51(4), 1299–1313.
  18. Li, R. (2021). Generalized alternating hyperharmonic number sums with reciprocal binomial coefficients. Journal of Mathematical Analysis and Applications, 504(1), Article ID 125397.
  19. Mansour, T., & Shattuck, M. (2014). A q-analog of the hyperharmonic numbers. Afrika Matematika, 25(1), 147–160.
  20. Nachlas, J. A. (2023). Probability Foundations for Engineers. CRC Press.
  21. Ömür, N., & Bilgin, G. (2018). Some applications of the generalized hyperharmonic numbers of order 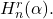r,H_{n}^{r} (\alpha ). Advances and Applications in Mathematical Sciences, 17(9), 617–627.
  22. Ömür, N., & Koparal, S. (2018). On the matrices with the generalized hyperharmonic numbers of order r. Asian-European Journal of Mathematics, 11(3), Article ID 1850045.
  23. Rim, S. H., Kim, T., & Pyo, S. S. (2018). Identities between harmonic, hyperharmonic and Daehee numbers. Journal of Inequalities and Applications, 2018(1), Article ID 168.

Manuscript history

  • Received: 9 June 2025
  • Revised: 18 November 2025
  • Accepted: 1 December 2025
  • Online First: 9 December 2025

Copyright information

Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Related papers

Cite this paper

Ömür, N., Koparal, S., & Duran, Ö. (2025). On q-generalized hyperharmonic numbers with two parameters. Notes on Number Theory and Discrete Mathematics, 31(4), 884-898, DOI: 10.7546/nntdm.2025.31.4.884-898.

Comments are closed.