Yangcheng Li and Hongjian Li
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 4, Pages 747–760
DOI: 10.7546/nntdm.2025.31.4.747-760
Full paper (PDF, 223 Kb)
Details
Authors and affiliations
Yangcheng Li ![]()
![]()
School of Mathematical Sciences, South China Normal University
Guangzhou 510631, Guangdong, P. R. China
Hongjian Li ![]()
![]()
School of Mathematics and Statistics, Guangdong University of Foreign Studies
Guangzhou 510006, Guangdong, P. R. China
Abstract
Let ![]() be the field of rational numbers, and let
be the field of rational numbers, and let ![]() be an algebraically closed field containing
be an algebraically closed field containing ![]() . Let
. Let ![]() be a polynomial, then the zero set of
be a polynomial, then the zero set of ![]() is
is ![]() . A set
. A set ![]() is called a
is called a ![]() -algebraic variety if
-algebraic variety if ![]() for some polynomial
for some polynomial ![]() in
in ![]() . The set
. The set ![]() is called the set of
is called the set of ![]() -rational points of
-rational points of ![]() . Let
. Let
![]()
be a vector function, where ![]() . It is easy to show that the function obtained by the composition of
. It is easy to show that the function obtained by the composition of ![]() and
and ![]() , denoted as
, denoted as ![]() , is still in
, is still in ![]() . Moreover, let
. Moreover, let ![]() be the set of
be the set of ![]() -rational points of the
-rational points of the ![]() -algebraic variety corresponding to
-algebraic variety corresponding to ![]() , i.e.,
, i.e., ![]() . A rational point
. A rational point ![]() is called a
is called a ![]() -point on
-point on ![]() if
if ![]() belongs to the intersection of
belongs to the intersection of ![]() and
and ![]() , that is
, that is ![]() . Denote
. Denote ![]() as the set consisting of all
as the set consisting of all ![]() -points on
-points on ![]() Obviously,
Obviously, ![]() is the set of
is the set of ![]() -rational points of a
-rational points of a ![]() -algebraic variety, that is,
-algebraic variety, that is, ![]() . In this paper, we consider the algebraic variety
. In this paper, we consider the algebraic variety ![]() for some specific functions
for some specific functions ![]() and
and ![]() . For these specific functions
. For these specific functions ![]() and
and ![]() , we prove that
, we prove that ![]() will be isomorphic to a certain elliptic curve. We also analyze some properties of these elliptic curves.
will be isomorphic to a certain elliptic curve. We also analyze some properties of these elliptic curves.
Keywords
- Algebraic varieties
- Elliptic curve
- Diophantine equation
- Rational solutions
2020 Mathematics Subject Classification
- 11D25
- 11D72
- 14A10
- 11G05
References
- Bennett, M. A. (2007). The Diophantine equation
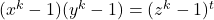 . Indagationes Mathematicae, 18(4), 507–525.
. Indagationes Mathematicae, 18(4), 507–525. - Katayama, S. (2006). On the Diophantine equation
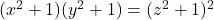 . Journal of Mathematics, Tokushima University, 40, 9–14.
. Journal of Mathematics, Tokushima University, 40, 9–14. - Schinzel, A., & Sierpiński, W. (1963). Sur l’équation diophantienne
![Rendered by QuickLaTeX.com (x^2-1)(y^2-1)=\Big [ \big( \frac{y-x}{2} \big)^2 -1 \Big ]^2](https://nntdm.net/wp-content/ql-cache/quicklatex.com-1ac9c5a532647f988fd385d24296dc25_l3.png) . Elemente der Mathematik, 18, 132–133.
. Elemente der Mathematik, 18, 132–133. - Sierpiński, W. (1964). Elementary Theory of Numbers. Wydawca Instytut Matematyczny Polskiej Akademii Nauk, Warszawa.
- Silverman, J. H., & Tate, J. (1992). Rational Points on Elliptic Curves. Springer.
- Ulas, M. (2007). On the diophantine equation
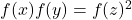 . Colloquium Mathematicum, 107(1), 1–6.
. Colloquium Mathematicum, 107(1), 1–6. - Ulas, M. (2008). On the diophantine equation
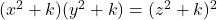 . Rocky Mountain Journal of Mathematics, 38, 2091–2097.
. Rocky Mountain Journal of Mathematics, 38, 2091–2097. - Zhang, Y. (2016). Some observations on the Diophantine equation
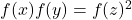 . Colloquium Mathematicum, 142(2), 275–284.
. Colloquium Mathematicum, 142(2), 275–284. - Zhang, Y. (2018). On the Diophantine equation
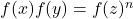 involving Laurent polynomials. Colloquium Mathematicum, 151(1), 111–122.
involving Laurent polynomials. Colloquium Mathematicum, 151(1), 111–122. - Zhang, Y., & Cai, T. (2013). On the Diophantine equation
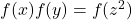 . Publicationes Mathematicae Debrecen, 82(1), 31–41.
. Publicationes Mathematicae Debrecen, 82(1), 31–41. - Zhang, Y., & Cai, T. (2015). A note on the Diophantine equation
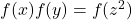 . Periodica Mathematica Hungarica, 70(2), 209–215.
. Periodica Mathematica Hungarica, 70(2), 209–215. - Zhang, Y., & Chen, D. (2020). A Diophantine equation about harmonic mean. Periodica Mathematica Hungarica, 80(1), 138–144.
- Zhang, Y., & Zargar, A. S. (2019). On the Diophantine equation
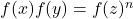 involving Laurent polynomials, II. Colloquium Mathematicum, 158(1), 119–126.
involving Laurent polynomials, II. Colloquium Mathematicum, 158(1), 119–126.
Manuscript history
- Received: 4 May 2025
- Accepted: 26 October 2025
- Online First: 28 October 2025
Copyright information
![]() Ⓒ 2025 by the Authors.
Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Li, Y., & Li, H. (2025). (G,F)-points on ℚ-algebraic varieties. Notes on Number Theory and Discrete Mathematics, 31(4), 747-760, DOI: 10.7546/nntdm.2025.31.4.747-760.


