I. Kátai, B. M. M. Khanh, B. M. Phong
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 4, Pages 718–727
DOI: 10.7546/nntdm.2025.31.4.718-727
Full paper (PDF, 225 Kb)
Details
Authors and affiliations
I. Kátai ![]()
![]()
Department of Computer Algebra, University of Eötvös Loránd
1117 Budapest, Hungary
B. M. M. Khanh ![]()
![]()
Department of Computer Algebra, University of Eötvös Loránd
1117 Budapest, Hungary
B. M. Phong ![]()
![]()
Department of Computer Algebra, University of Eötvös Loránd
1117 Budapest, Hungary
Abstract
We prove that if ![]() is a completely multiplicative function and
is a completely multiplicative function and ![]() such that the equation
such that the equation ![]() holds for every
holds for every ![]() ,
, ![]() then
then ![]() is the identity function. A similar result is proved for the equation
is the identity function. A similar result is proved for the equation ![]() assuming a suitable conjecture concerning prime numbers. The equation
assuming a suitable conjecture concerning prime numbers. The equation ![]() is also studied.
is also studied.
Keywords
- Completely multiplicative function
- Identity function
- Functional equation
- Dirichlet character
2020 Mathematics Subject Classification
- 11A07
- 11A25
- 11N25
- 11N64
References
- Kátai, I., Khanh, B. M. M., & Phong, B. M. (2023). On the equation
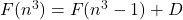 and some conjectures. Publicationes Mathematicae Debrecen, 103(1–2), 257–267.
and some conjectures. Publicationes Mathematicae Debrecen, 103(1–2), 257–267. - Kátai, I., Khanh, B. M. M., & Phong, B. M. (2025). On the equation
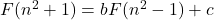 . Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae. Sectio Computatorica, 58, 177–189.
. Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae. Sectio Computatorica, 58, 177–189.
Manuscript history
- Received: 12 June 2025
- Revised: 28 September 2025
- Accepted: 1 October 2025
- Online First: 12 October 2025
Copyright information
![]() Ⓒ 2025 by the Authors.
Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Kátai, I., Khanh, B. M. M., & Phong, B. M. (2025). On the equation ![]() . Notes on Number Theory and Discrete Mathematics, 31(4), 718-727, DOI: 10.7546/nntdm.2025.31.4.718-727.
. Notes on Number Theory and Discrete Mathematics, 31(4), 718-727, DOI: 10.7546/nntdm.2025.31.4.718-727.


