Extending the plane trigonometric proof of Fermat’s Last Theorem to the case n = 3

Giri Prabhakar
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 2, Pages 410–428
DOI: 10.7546/nntdm.2025.31.2.410-428
Full paper (PDF, 1756 Kb)

Details

Authors and affiliations

Giri Prabhakar
Siemens Technology
Electronics City Phase 2, Bangalore 560100, India

Abstract

We extend the plane trigonometric approach that we used to prove the case n = 4 of Fermat’s Last Theorem, to the case n=3. We show that all real positive triplets satisfying a^\phi + b^\phi = c^\phi for \phi > 1 are triangles. As in the case of n=4, we equate the Pythagorean and Fermat descriptions of the triangles for a particular smaller side while fixing the other sides, with \phi=n being any positive integer. We hence show the existence of Fermat–Pythagoras polynomials for n \ge 3. For the case n=3, we explicitly derive an analytic expression for the roots of the polynomials. We prove from this expression that the real roots, which are equal to the length of the sides, are irrational.

Keywords

  • Pythagorean theorem
  • Diophantine equations
  • Fermat’s Last Theorem

2020 Mathematics Subject Classification

  • 51N20
  • 11D41

References

  1. Aliprantis, C. D., & Burkinshaw, O. (1998). Principles of Real Analysis. Academic Press Inc., San Diego.
  2. Barany, M. J. (2013). Stuck in the Middle: Cauchy’s Intermediate Value Theorem and the history of analytic rigor. Notices of the American Mathematical Society, 60(10), 1334–1338.
  3. Barbara, R. (2017). 101.01 Fermat’s last theorem for n = 3 revisited. The Mathematical Gazette, 101(550), 90–93.
  4. Dolan, S. (2011). 95.24 Fermat’s method of “descente infinie”. The Mathematical Gazette, 95(533), 269—271.
  5. Edwards, H. M. (2000). Fermat’s Last Theorem: A Genetic Introduction to Algebraic Number Theory. Springer-Verlag, New York.
  6. Gauss, C. F., & Clarke, A. A. (1965). Article 42. In Disquisitiones Arithmeticae (p. 25). Yale University Press.
  7. Heath, T. L. (1925). The Thirteen Books of Euclid’s Elements (2nd ed.). Dover Publications, New York 1, 286–287.
  8. De Oliveira, O. R. B. (2012). The fundamental theorem of algebra: From the four basic operations. The American Mathematical Monthly, 119, 753–758.
  9. Prabhakar, G. (2021). A plane trigonometric proof for the case n = 4 of Fermat’s Last Theorem. Notes on Number Theory and Discrete Mathematics, 27(4), 154–163.
  10. Ribenboim, P. (2000). Fermat’s Last Theorem for Amateurs. Springer-Verlag, New York.
  11. Sastry, S. (2004). Engineering Mathematics. PHI Learning.
  12. Wiles, A. (1995). Modular elliptic curves and Fermat’s Last Theorem. Annals of Mathematics, 141(3), 443—551.
  13. Wolfram Research, Inc., Wolfram—Alpha, Champaign, IL (2024). WolframAlpha [“solve(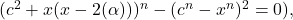(c^2 + x(x-2(\alpha)))^n-(c^n-x^n)^2=0), for c=15,\alpha=7,n=7“,
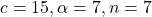    HTTP Link for Root Plot] (access June 14, 2025).

Manuscript history

  • Received: 26 June 2024
  • Revised: 7 May 2025
  • Accepted: 4 June 2025
  • Online First: 16 June 2025

Copyright information

Ⓒ 2025 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Related papers

Cite this paper

Prabhakar, G. (2025). Extending the plane trigonometric proof of Fermat’s Last Theorem to the case n = 3. Notes on Number Theory and Discrete Mathematics, 31(2), 410-428, DOI: 10.7546/nntdm.2025.31.2.410-428.

Comments are closed.