A note on the density of the Greatest Prime Factor

Rafael Jakimczuk
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 19, 2013, Number 1, Pages 55–58
Full paper (PDF, 148 Kb)

Details

Authors and affiliations

Rafael Jakimczuk
División Matemática, Universidad Nacional de Luján
Buenos Aires, Argentina

Abstract

Let P(n) be the greatest prime factor of a positive integer n ≥ 2. Let L (n) be the number of 2 ≤ k ≤ n such that P(k) > kα, where 0 < α < 1. We prove the following asymptotic formula
L_{\alpha}(n)=(1-\rho(\alpha))n+O\left(\frac{n}{\log n}\right),
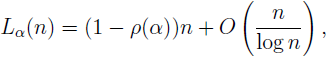
where ρ(α) is the Dickman’s function.

Keywords

  • Greatest prime factor
  • Distribution

AMS Classification

  • 11A99
  • 11B99

References

  1. Kemeny, J. Largest prime factor, J. Pure Appl. Algebra, Vol. 89, 1993, 181–186.
  2. LeVeque, W. J. Topics in Number Theory, Addison-Wesley, 1958.
  3. Ramaswami, R. On the number of positive integers less than x and free of prime divisors greater than xc, Bull. Amer. Math. Soc., Vol. 55, 1949, 1122–1127.

Related papers

Cite this paper

Jakimczuk, R. (2013). A note on the density of the Greatest Prime Factor. Notes on Number Theory and Discrete Mathematics, 19(1), 55-58.

Comments are closed.