Volume 4, 1998, Number 1

Volume 4 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

The characteristics of primes and other integers within the modular ring Z₄ and in Class 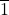$\overline{1}$
Original research paper. Pages 1–17
J. V. Leyendekkers, J. M. Rybak and A. G. Shannon
Full paper (PDF, 663 Kb) | Abstract

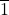
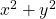
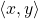
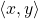
The integer structure of Class $\overline{1}$ in the modular ring Z₄ has been analysed in detail. Most integers of this category equal a sum of two squares ( $x^2 + y^2$ ). Those that do not are non-primes. The primes are distinguished by having a unique $\langle x, y \rangle$ pair that has no common factors. 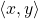Other integers in Class $\overline{1}$ have multiple values of $\langle x, y \rangle$ or more rarely a single $\langle x, y \rangle$ pair with common factors. 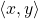Methods of estimating $\langle x, y \rangle$ pairs are given. These are based on the class structure within Z₄ and the right-most end digit characteristics. The identification of primes is consequently facilitated.

The characteristics of primes and other integers within the modular ring Z₄ and in class 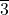$\overline{3}$
Original research paper. Pages 18–37
J. V. Leyendekkers, J. M. Rybak and A. G. Shannon
Full paper (PDF, 911 Kb) | Abstract

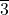
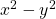
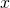
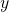
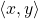
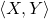
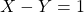
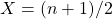
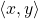
Integers, n, in Class $\overline{3}$ of the modular ring Z₄ have been analysed in detail. All n equal the difference of squares, $x^2 - y^2$ , with $x$ even and $y$ odd. Primes are distinguished by having only one $\langle x, y \rangle$ pair: $\langle X, Y \rangle$ with $X - Y = 1$ , and $X = (n + 1) / 2$ . In this paper four methods of calculating the $\langle x, y \rangle$ values are given. These methods are based on prime factorisation, the Z₄ class structure, and Fermat’s Little Theorem. 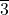Mersenne primes are uniquely distributed within Class $\overline{3}$ and some new features of these primes are also stated.

Numerical properties of Morgan-Voyce Numbers
Original research paper. Pages 38–42
A. F. Horadam
Full paper (PDF, 163 Kb)

One extremal problem. 8
Original research paper. Pages 43–44
Krassimir T. Atanassov
Full paper (PDF, 131 Kb)

Volume 4 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Latest Issue

Journal Contents