József Sándor
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 3, Pages 583–587
DOI: 10.7546/nntdm.2025.31.3.583-587
Full paper (PDF, 191 Kb)
Details
Authors and affiliations
József Sándor 
Department of Mathematics, Babeș-Bolyai University
Cluj-Napoca, Romania
Abstract
We offer new proof and refinement of a double inequality for 
by L. R. Shenton and A. W. Kemp [11].
Keywords
- Inequalities
- Series expansions
- Means
2020 Mathematics Subject Classification
- 26D05
- 26D99
References
- Carlson, B. C. (1972). The logarithmic mean. The American Mathematical Monthly, 79(6), 615–618.
- Leach, E. B., & Sholander, M. C. (1983). Extended mean values II. Journal of Mathematical Analysis and Applications, 92(1), 207–223.
- Lin, T.-P. (1974). The power mean and the logarithmic mean. The American Mathematical Monthly, 81(8), 879–883.
- Pólya, G., & Szegő, G. (1951). Isoperimetric Inequalities in Mathematical Physics. Princeton University Press.
- Sándor, J. (1988). Some integral inequalities. Elemente der Mathematik, 43(6), 177–180.
- Sándor, J. (1990). On the identric and logarithmic means. Aequationes Mathematicae, 40, 261–270.
- Sándor, J. (2015). A basic logarithmic inequality, and the logarithmic mean. Notes on Number Theory and Discrete Mathematics, 21(1), 31–35.
- Sándor, J. (2016). A note on the logarithmic mean. The American Mathematical Monthly, 123(1), 112.
- Sándor, J. (2016). Series expansions related to the logarithmic mean. Notes on Number Theory and Discrete Mathematics, 22(2), 54–57.
- Sándor, J., & Bhayo, B. A. (2018). On two new means of two arguments III. Problemy Analiza — Issues of Analysis, 7(25), 1, 116–133.
- Shenton, L. R., & Kemp, A. W. (1989). An S-fraction and
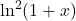. Journal of Computational and Applied Mathematics, 25(1), 121–124.
Manuscript history
- Received: 10 May 2025
- Accepted: 20 August 2025
- Online First: 1 September 2025
Copyright information
Ⓒ 2025 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Sándor, J. (2016). Series expansions related to the logarithmic mean. Notes on Number Theory and Discrete Mathematics, 22(2), 54–57.
- Sándor, J. (2015). A basic logarithmic inequality, and the logarithmic mean. Notes on Number Theory and Discrete Mathematics, 21(1), 31–35.
Cite this paper
Sándor, J. (2025). On a logarithmic inequality by Shenton and Kemp. Notes on Number Theory and Discrete Mathematics, 31(3), 583-587, DOI: 10.7546/nntdm.2025.31.3.583-587.
