Narendra Bhandari
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 3, Pages 613–633
DOI: 10.7546/nntdm.2024.30.3.613-633
Full paper (PDF, 314 Kb)
Details
Authors and affiliations
Narendra Bhandari ![]()
![]()
Department of Mathematics, Rajdhani College, University of Delhi
New Delhi, India
Budiganga-01, Bajura, Sudurpaschim Province, Nepal
Abstract
We consider a polylogarithm expression containing complex arguments, namely
![]()
The central notion of the present paper is to evaluate the real parts of ![]() for first four orders, specifically
for first four orders, specifically ![]() and
and ![]() by constructing certain logarithmic integrals. To extract the real parts, we demonstrate an organized approach, and the proofs solely rely on the calculation of the logarithmic integrals. Additionally, we present a potential closed form of
by constructing certain logarithmic integrals. To extract the real parts, we demonstrate an organized approach, and the proofs solely rely on the calculation of the logarithmic integrals. Additionally, we present a potential closed form of ![]()
Keywords
- Polylogarithm function
- Dilogarithm function
- Logarithmic integral
- Real part
- Harmonic number
- Gamma function
- Beta function
2020 Mathematics Subject Classification
- 33B30
- 40C10
- 33B15
References
- Adamchik, V. S. (2002). A certain series associated with Catalan’s constant. Journal of Analysis and its Application, 21(3), 817–826.
- Au, K. C. (2022). Mathematica package multiple zeta values. Preprint. Available online at: https://www.researchgate.net/publication/357601353.
- Bastien, G. Elementary methods for evaluating Jordan’s sums
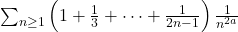 and
and  and analogous Euler’s type sums and for setting a
and analogous Euler’s type sums and for setting a 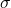 –sum theorem. Preprint. Available online at: https://arxiv.org/abs/1301.7662.
–sum theorem. Preprint. Available online at: https://arxiv.org/abs/1301.7662. - Bradley, D. V. (2001). Representations of Catalan’s constant. Preprint. Available online at: https://www.researchgate.net/publication/2325473.
- Campbell, J. M., Levrie, P., & Nimbran, A. S. (2021). A natural companion to Catalan’s constant. Journal of Classical Analysis, 18(2), 117–135.
- Chen, K. (2020). On the relationship between
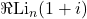 and
and 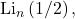 when
when 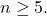 Available online at: https://math.stackexchange.com/questions/3447529.
Available online at: https://math.stackexchange.com/questions/3447529. - Gradshteyn, I. S., & Ryzhik, I. M. (2007). Table of Series, Integrals, and Products (7th Ed.). Academic Press, Elsevier.
- Lewin, L. (1981). Polylogarithms and Associated Functions. North Holland, New York.
- Olaikhan, A. S. (2023). An Introduction to the Harmonic Series and Logarithmic Integrals. Phoenix, AZ.
- Shadhar, A. (2020). How to find
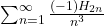 and
and 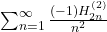 using real methods?. Available online at: https://math.stackexchange.com/questions/3803424.
using real methods?. Available online at: https://math.stackexchange.com/questions/3803424. - Sofo, A., & Nimbran, A. S. (2020). Euler-like sums via powers of log, arctan, and arctanh functions. Integral Transforms and Special Functions, 31, 966–981.
- Stewart, S. M. (2020). Explicit Evaluation of some quadratic Euler-type sums containing double-index harmonic numbers. Tatra Mountains Mathematical Publications, 77, 73–98.
- Vălean, C. I. (2019). (Almost) Impossible Integrals, Sums, and Series. Springer, New York.
- Vălean, C. I. (2023). More (Almost) Impossible Integrals, Sums, and Series. Springer, New York.
- Vălean, C. I. (2019). A special way of extracting the real part of the Trilogarithm,
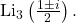 Preprint. Available online at: https://www.researchgate.net/publication/337868999.
Preprint. Available online at: https://www.researchgate.net/publication/337868999. - Vălean, C. I. (2019). A simple strategy of calculating two alternating harmonic series generalizations. Preprint. Available online at: https://www.researchgate.net/publication/333339272.
- Zhao, M. H. (2020). On logarithmic integrals, harmonic sums and variations. Preprint. Available online at: https://arxiv.org/abs/1911.12155.
Manuscript history
- Received: 6 August 2023
- Revised: 25 June 2024
- Accepted: 22 October 2024
- Online First: 24 October 2024
Copyright information
![]() Ⓒ 2024 by the Author.
Ⓒ 2024 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Bhandari, N. (2024). Evaluation of the real parts of polylogarithm expressions containing complex arguments via certain logarithmic integrals. Notes on Number Theory and Discrete Mathematics, 30(3), 613-633, DOI: 10.7546/nntdm.2024.30.3.613-633


