Euler sine product and the continued fraction of π

Rahul Verma, V. Puneeth, Joseph Varghese Kureethara and Ashish Sharma
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 3, Pages 463–478
DOI: 10.7546/nntdm.2024.30.3.463-478
Full paper (PDF, 3702 Kb)

Details

Authors and affiliations

Rahul Verma
School of Sciences, CHRIST University Delhi-NCR
Ghaziabad 201003, India

V. Puneeth
Department of Mathematics, CHRIST University
Bengaluru 560029, India

Joseph Varghese Kureethara
Department of Mathematics, CHRIST University
Bengaluru 560029, India

Ashish Sharma
School of Sciences, CHRIST University Delhi-NCR
Ghaziabad 201003, India

Abstract

The Euler sine product and the continued fraction of \pi are discussed in this article. Some of the infinite series for cotangent and its derivative are obtained by implementing the concept of Euler sine product and some of the standard series are derived as the immediate consequence of the main results. Furthermore, the continued fraction for odd powers of \pi similar to the expression of \pi derived by Brouncker is presented in this article. Meanwhile, an expression relating the Basel’s constant and the cotangent function is obtained as follows:

    \begin{equation*} \frac{\coth{r}}{2}-\frac{1}{2r}=\sum_{n\in\mathbb{N}}\frac{2^{2n}}{2(2n)!}B_{2n}r^{2n-1}. \end{equation*}

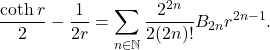
Keywords

  • Euler product
  • Continued fraction
  • Basel constants
  • Series

2020 Mathematics Subject Classification

  • 11A41
  • 11A55
  • 11A67

References

  1. Ayoub, R. (1974). Euler and the zeta function. The American Mathematical Monthly, 81(10), 1067–1086.
  2. Debnath, L. (2009). The legacy of Leonhard Euler–a tricentennial tribute. International Journal of Mathematical Education in Science and Technology, 40(3), 353–388.
  3. Dutka, J. (1982). Wallis’s product, Brouncker’s continued fraction, and Leibniz’s series. Archive for History of Exact Sciences, 26, 115–126.
  4. Holst, L. (2012). A Proof of Euler’s Infinite Product for the Sine. The American Mathematical Monthly, 119(6), 518–521.
  5. Kim, T. (2008). Euler numbers and polynomials associated with zeta functions. Abstract and Applied Analysis, 2008.
  6. Kim, T., & Kim, D. S. (2022). A new approach to fully degenerate Bernoulli numbers and polynomials. arXiv preprint arXiv:2203.03855
  7. Kim, T., & Kim, D. S. (2024). Probabilistic Bernoulli and Euler polynomials. Russian Journal of Mathematical Physics, 31(1), 94–105.
  8. Kim, T., Kim, D. S., Kwon, J., & Pyo, S. S. (2022). A note on identities involving special numbers and moments of poisson random variable. Advanced Studies in Contemporary Mathematics, 32(4), 457–464.
  9. Kim, T., Kim, D. S., & Park, J.-W. (2022). Fully degenerate Bernoulli numbers and polynomials. Demonstratio Mathematica, 55(1), 604–614.
  10. Lange, L. J. (1999). An elegant continued fraction for π. The American Mathematical Monthly, 106(5), 456–458.
  11. Nimbran, A. S. (2014). Generalized Wallis–Euler products and new infinite products for π. The Mathematics Student, 83, 155–164.
  12. Oscar, C. (2015). Euler’s Product Expansion for the Sine: An Elementary Proof. The American Mathematical Monthly, 122(7), 693–695.
  13. Osler, T. J. (2011). Morphing Lord Brouncker’s continued fraction for π into the product of Wallis. The Mathematical Gazette, 95(532), 17–22.
  14. Sandifier, S. E. (2007). Euler’s solution of the Basel problem—the longer story. Euler at 300: An Appreciation, 105–117.
  15. Sofo, A. (2018). The Basel problem with an extension. Mathematical Analysis and Applications: Selected Topics, 631–659.
  16. Varadarajan, V. (2007). Euler and his work on infinite series. Bulletin of the American Mathematical Society, 44(4), 515–539.

Manuscript history

  • Received: 12 September 2023
  • Revised: 25 August 2024
  • Accepted: 27 August 2024
  • Online First: 28 August 2024

Copyright information

Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Related papers

Cite this paper

Verma, R., Puneeth, V., Kureethara, J. V., & Sharma, A. (2024). Euler sine product and the continued fraction of π. Notes on Number Theory and Discrete Mathematics, 30(3), 463-478, DOI: 10.7546/nntdm.2024.30.3.463-478.

Comments are closed.