On certain relations among the generating functions for certain quadratic forms

K. R. Vasuki and P. Nagendra
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 2, Pages 418–426
DOI: 10.7546/nntdm.2024.30.2.418-426
Full paper (PDF, 213 Kb)

Details

Authors and affiliations

K. R. Vasuki
Department of Studies in Mathematics, University of Mysore
Manasagangothri Campus, Mysuru – 570006, India

P. Nagendra
Department of Studies in Mathematics, University of Mysore
Manasagangothri Campus, Mysuru – 570006, India

Abstract

The object of this article is to establish the relation between the generating function of the quadratic form 2m^2+2mn+3n^2 {and} the generating function{s} for the quadratic forms m^2+mn+n^2, m^2+mn+2n^2, m^2+mn+4n^2 and 2m^2+mn+2n^2. In the process, we deduce certain interesting theta function identities.

Keywords

  • Eisenstein series
  • Quadratic forms
  • Theta functions

2020 Mathematics Subject Classification

  • 11E25
  • 11M36

References

  1. Alaca, A. (2018). Representations by quaternary quadratic forms with coefficients 1, 3, 5 or 15. Integers, 18, Article A12.
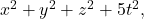
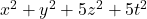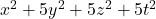  2. Alaca, A., Alaca, Ş., & Williams, K. S. (2007). On the quaternary forms x^2 + y^2 + z^2 + 5t^2, x^2 +y^2 +5z^2 +5t^2 and x^2 +5y^2 +5z^2 +5t^2. JP Journal of Algebra Number Theory and Applications, 9(1), 37–53.
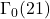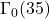  3. Anusha, T., Bhuvan, E. N., Cooper, S., & Vasuki, K. R. (2019). Elliptic integrals associated with \Gamma_0(21) and \Gamma_0(35) and the corresponding Ramanujan-type series for 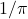1/\pi. Journal of Mathematical Analysis and Applications, 472(2), 1551–1570.
  4. Berndt, B. C. (1991). Ramanujan Notebooks, Part III. Springer-Verlag, New York.
  5. Berndt, B. C. (1991). Ramanujan Notebooks, Part V. Springer-Verlag, New York.
  6. Borwein, J. M., & Borwein, P. B. (1991). A cubic counterpart of Jacobi’s identity and the AGM. Transactions of the American Mathematical Society, 323(2), 691–701.
  7. Cooper, S. (2017). Ramanujan’s Theta Functions. Springer, New York.
  8. Cooper, S., & Ye, D. (2016). Level 14 and 15 analogues of Ramanujan’s elliptic functions to alternative bases. Transactions of the American Mathematical Society, 368, 7883–7910.
  9. Kang, S. Y. (1999). Some theorems on the Rogers–Ramanujan continued fraction and associated theta function identities in Ramanujan’s lost notebook. Ramanujan Journal, 3, 91–111.
  10. Lorenz, L. (1871). Bidrag til tallenes theori. Tidsskrift for Mathematik, 1, 97–114.
  11. Ramanujan, S. (1957). Notebooks (2 Volumes). Tata Institute of Fundamental Research, Bombay.
  12. Veeresha, R. G. (2015). An elementary approach to Ramanujan’s modular equations of degree 7 and its applications. Doctoral Thesis, University of Mysore, Mysuru, India. Available online at: http://hdl.handle.net/10603/108538
  13. Williams, K. S. (2011). Number Theory in the Spirit of Liouville. London Mathematical Society Student Texts, 76, Cambridge University Press, Cambridge.
  14. Williams, K. S. (2017). Some arithmetic convolution identities. Ramanujan Journal, 43, 197–213.

Manuscript history

  • Received: 4 October 2023
  • Revised: 15 May 2024
  • Accepted: 18 June 2024
  • Online First: 18 June 2024

Copyright information

Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Related papers

Cite this paper

Vasuki, K. R., & Nagendra, P. (2024). On certain relations among the generating functions for certain quadratic forms. Notes on Number Theory and Discrete Mathematics, 30(2), 418-426, DOI: 10.7546/nntdm.2024.30.2.418-426.

Comments are closed.