Carlos M. da Fonseca and Anthony G. Shannon
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 3, Pages 557–563
DOI: 10.7546/nntdm.2023.29.3.557-563
Full paper (PDF, 350 Kb)
Details
Authors and affiliations
Carlos M. da Fonseca ![]()
![]()
Kuwait College of Science and Technology,
Doha District, Safat 13133, Kuwait
Chair of Computational Mathematics, University of Deusto
48007 Bilbao, Spain
Anthony G. Shannon ![]()
Honorary Fellow, Warrane College, University of New South Wales, 2033, Australia
Abstract
Recently, based on the Laplace transform of the characteristic polynomial of the Fibonacci sequence, Deveci and Shannon established a new sequence and analysed some of its properties. They disclosed in particular the odd terms. In this short note, we provide a matricial representation for this sequence as well as one in terms of the Chebyshev polynomials of the second kind. The subsequence of the even terms is also disclosed.
Keywords
- Fibonacci sequence
- Recurrence
- Chebyshev polynomials of the second kind
- Determinant
- Tridiagonal matrices
2020 Mathematics Subject Classification
- 11B37
- 11B39
- 15A15
References
- Aharonov, D., Beardon, A., & Driver, K. (2005). Fibonacci, Chebyshev, and orthogonal polynomials. The American Mathematical Monthly, 112, 612–630.
- Anđelić, M., Du, Z., da Fonseca, C. M., & Kılıç, E. (2020). Second-order difference equations with sign-alternating coefficients. Journal of Difference Equations and Applications, 26, 149–162.
- Anđelić, M., & da Fonseca, C. M. (2021). Determinantal representations for the number of subsequences without isolated odd terms. Notes on Number Theory and Discrete Mathematics, 27(4), 116–121.
- Anđelić, M., & da Fonseca, C. M. (2021). On the constant coefficients of a certain recurrence relation: A simple proof. Heliyon, 7, Article ID E07764.
- Anđelić, M., da Fonseca, C. M., & Yılmaz, F. (2022). The bi-periodic Horadam sequence and some perturbed tridiagonal 2-Toeplitz matrices: A unified approach. Heliyon, 8, Article ID E08863.
- Buschman, R. G. (1963). Fibonacci numbers, Chebyshev polynomials generalizations and difference equations. The Fibonacci Quarterly, 1, 1–8, 19.
- Cvetković, A., Rajković, P., & Ivković, M. (2002). Catalan numbers, the Hankel transform, and Fibonacci numbers. Journal of Integer Sequences, 5, Article ID 02.1.3.
- Deveci, Ö., & Shannon, A. G. (2022). On recurrence results from matrix transforms. Notes on Number Theory and Discrete Mathematics, 28(4), 589–592.
- Du, Z., Dimitrov, D., & da Fonseca, C. M. (2021). New strong divisibility sequences. Ars Mathematica Contemporanea, 22(1), Article ID P1.08.
- Dumont, D. (1974). Interprétations combinatoires des nombres de Genocchi. Duke Mathematical Journal, 41, 305–318.
- Estrada, E., & de la Peña, J. A. (2013). Integer sequences from walks in graphs. Notes on Number Theory and Discrete Mathematics, 19(3), 78–84.
- Flegg, G. (1983). Numbers: Their History and Meaning. Schocken Books, New York.
- Da Fonseca, C. M. (2020). On the connection between tridiagonal matrices, Chebyshev polynomials, and Fibonacci numbers. Acta Universitatis Sapientiae Mathematica, 12, 280–286.
- Da Fonseca, C. M. (2014). Unifying some Pell and Fibonacci identities. Applied Mathematics and Computation, 236, 41–42.
- Gould, H. W. (1972). Combinatorial Identities. Morgantown: Morgantown Printing and Binding Co.
- Hong, S., & Kwak, J. H. (1993). Regular fourfold coverings with respect to the identity automorphism. Journal of Graph Theory, 17, 621–627.
- Horadam, A. F. (1965). Generating functions for powers of a certain generalised sequence of numbers. Duke Mathematical Journal, 32(3), 437–446.
- Horadam, A. F. (1969). Tschebyscheff and other functions associated with the sequence
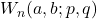 . The Fibonacci Quarterly, 7, 14–22.
. The Fibonacci Quarterly, 7, 14–22. - Horadam, A. F., & Shannon, A. G. (1987). Generalization of identities of Catalan and others. Portugaliae Mathematica, 44(2), 137–148.
- Melham, R. S., & Shannon, A. G. (1995). On reciprocal sums of Chebyshev related
sequences. The Fibonacci Quarterly, 33(2), 194–202. - Shannon, A. G. (1975). Fibonacci analogs of the classical polynomials. Mathematics Magazine, 48(3), 123–130.
- Singh, P. (1985). The so-called Fibonacci numbers in ancient and medieval India. Historia Mathmatica, 12(3), 229–244.
- Thiele, T. N. (1909). Interpolationsrechnung. Leipzig: B. G. Teubner.
- Udrea, G. (1996). A note on the sequence
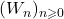 of A. F. Horadam. Portugaliae
of A. F. Horadam. Portugaliae
Mathematica, 53(2), 143–155.
Manuscript history
- Received: 11 February 2023
- Revised: 18 July 2023
- Accepted: 29 July 2023
- Online First: 30 July 2023
Copyright information
![]() Ⓒ 2023 by the Authors.
Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Anđelić, M., & da Fonseca, C. M. (2021). Determinantal representations for the number of subsequences without isolated odd terms. Notes on Number Theory and Discrete Mathematics, 27(4), 116–121.
- Deveci, Ö., & Shannon, A. G. (2022). On recurrence results from matrix transforms. Notes on Number Theory and Discrete Mathematics, 28(4), 589–592.
- Estrada, E., & de la Peña, J. A. (2013). Integer sequences from walks in graphs. Notes on Number Theory and Discrete Mathematics, 19(3), 78–84.
Cite this paper
Da Fonseca, C. M., & Shannon, A. G. (2023). On a sequence derived from the Laplace transform of the characteristic polynomial of the Fibonacci sequence. Notes on Number Theory and Discrete Mathematics, 29(3), 557-563, DOI: 10.7546/nntdm.2023.29.3.557-563.


