Necdet Batır and Anthony Sofo
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 1, Pages 78–97
DOI: 10.7546/nntdm.2023.29.1.78-97
Full paper (PDF, 299 Kb)
Details
Authors and affiliations
Necdet Batır ![]()
![]()
![]()
Department of Mathematics, Nevşehir Hacı Bektaş Veli University, Turkey
Anthony Sofo ![]()
![]()
College of Engineering and Science, Victoria University, Australia
Abstract
We offer a number of various finite and infinite sum identities involving the binomial coefficients, Bernoulli numbers of the second kind and harmonic numbers. For example, among many others, we prove
![Rendered by QuickLaTeX.com \[\displaystyle \sum_{k=0}^{n}\frac{(-1)^{k}h_{k}}{4^{k}} {{2k} \choose {k}}G_{n-k}=\frac{(-1)^{n-1}}{2^{2n-1}}{{2n-2} \choose {n-1}}\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-d8a55db4281e9f43631243f9b2c0b991_l3.png)
and
![Rendered by QuickLaTeX.com \[\displaystyle \sum_{k=1}^{\infty}\frac{h_{k}}{k^{2}(2k-1)4^{k}} {{2k} \choose {k}}=2\pi +3\zeta(2)\log 2-3\zeta(2)-\frac{7}{2}\zeta(3),\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-7686fb941e20c40fa5d553f9f1f548f5_l3.png)
where ![]()
![]() are Bernoulli numbers of the second kind, and
are Bernoulli numbers of the second kind, and ![]() is the Riemann zeta function. We also give an alternate proof of the series representations for the constants
is the Riemann zeta function. We also give an alternate proof of the series representations for the constants ![]() and
and ![]() given by Blagouchine and Coppo.
given by Blagouchine and Coppo.
Keywords
- Binomial sums
- Harmonic sums
- Binomial coefficients
- Gregory coefficients
- Bernoulli numbers of the second kind
- Polygamma functions
- Riemann zeta function
- Harmonic numbers
2020 Mathematics Subject Classification
- 05A10
- 05A19
References
- Alabdulmohsin, I. M (2012). Summability calculus. arXiv:1209.5739.
- Alabdulmohsin, I. M. (2018). Summability Calculus: A Comprehensive Theory of Fractional Finite Sums. Springer International Publishing.
- Alzer, H., & Nagy, G. V. (2020). Sum identities involving central Binomial coefficients and Catalan numbers. Integers, 20, Article 59.
- Batır, N. (2017). On some combinatorial identities and harmonic sums. International Journal of Number Theory, 13(7), 1695–1709.
- Batır, N. (2020). Combinatorial identities involving harmonic numbers. Integers, 20, Article 25.
- Batır, N., Küçük, H., & Sorgun, S. (2021). Convolution identities involving the central binomial coefficients and Catalan numbers. Transactions on Combinatorics, 10(4), 225–238.
- Blagouchine, Ia. V. (2018). Three notes on Ser’s and Hasse’s representations for the zeta-functions. Integers, 18A, Article 43.
- Blagouchine, Ia V. (2016). Expansions of generalized Euler’s constants into the series of polynomials in
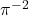 and into the formal enveloping series with rational coefficients only. Journal of Number Theory, 158, 365–396.
and into the formal enveloping series with rational coefficients only. Journal of Number Theory, 158, 365–396. - Blagouchine, Ia V. (2016). Corrigendum to “Expansions of generalized Euler’s constants into the series of polynomials in
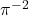 and into the formal enveloping series with rational coefficients only” [J. Number Theory 158 (2016) 365–396]. Journal of Number Theory, 173, 631–632.
and into the formal enveloping series with rational coefficients only” [J. Number Theory 158 (2016) 365–396]. Journal of Number Theory, 173, 631–632. - Blagouchine, Ia. V. (2017). A note on some recent results for the Bernoulli numbers of the second kind. Journal of Integer Sequences, 20, Article 17.3.8.
- Blagouchine, Ia. V., & Coppo, M.-A. (2018). A note on some constants related to the zeta-function and their relationship with the Gregory coefficients. Ramanujan Journal, 47, 457–473.
- Boyadzhiev, K. N. (2018). Notes on the Binomial Transform. World Scientific.
- Boyadzhiev, K. N. (2020). New series identities with Cauchy, Stirling, and harmonic numbers, and Laguerre polynomials. Journal of Integer Sequences, 23, Article 21.11.7.
- Candelpergher, B., & Coppo, M.-A. (2012). A new class of identities involving Cauchy numbers, harmonic numbers and zeta values. Ramanujan Journal, 27, 305–328.
- Chu, W. (2012). Summation formulae involving harmonic numbers. Filomat, 26(1), 143–152.
- Coffey, M. W. (2012). Certain integrals, including solution of Monthly problem, zeta values, and expressions for the Stieltjes constants. Preprint. arxiv:1201.3393v1.
- Euler, L. (1799/1802) Demonstratio insignis theorematis numerici circa uncias potestatum binomialium. Nova Acta Academiae Scientiarum Imperialis Petropolitanae, 15, 33–43.
- Graham, R. L., Knuth, D. E., & Patashnik, O. (1994). Concrete Mathematics (2nd ed.). New York: Addison-Wesley.
- Jordan, C. (1947). The Calculus of Finite Differences. Chelsea Publishing Company, USA.
- Jordan, C. (1928). Sur des polynomes analogues aux polynomes de Bernoulli, et sur des formules de sommation analogues à celle de Maclaurin–Euler. Acta Scientiarum Mathematicarum (Szeged), 4, 130–150.
- Kurtz, D. S., & Swartz, C. W. (2004). Theories of Integration. Series in Real Analysis (Vol. 9). World Scientific.
- Merlini, D., Sprugnoli, R., & Verri, C. (2006). The Cauchy numbers. Discrete Mathematics, 306, 1906–1920.
- Nemes, G. (2011). An asymptotic expansion for the Bernoulli numbers of the second kind. Journal of Integer Sequences, 14, Article 11.4.8.
- Nörlund, N. E. (1924). Vorlesungen über Differenzenrechnung. Berlin: Springer.
- Sato, H. (2008). On a relation between the Riemann zeta function and the Stirling numbers. Integers, 8, Article 53.
- Shen, L-C. (1995). Remarks on some integrals and series involving the Stirling numbers and
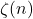 . Transactions of the American Mathematical Society, 347(4), 1391–1399.
. Transactions of the American Mathematical Society, 347(4), 1391–1399. - Slavić, D. V. (1975). On coefficients of the Gregory formula. Publikacije Elektrotehničkog fakulteta. Serija Matematika i Fizika, 498/541, 27–32.
- Sofo, A., & Srivastava, H. M. (2015). A family of shifted harmonic sums. Ramanujan Journal, 37(1), 89–108.
- Sofo, A., & Cvijović, D. (2012). Extensions of Euler harmonic sums. Applicable Analysis and Discrete Mathematics, 6(2), 317–328.
- Sofo, A. (2014). Shifted harmonic sums of order two. Communications of the Korean Mathematical Society, 29(2), 239–255.
- Srivastava, H. M., & Choi, J. (2012). Zeta and 𝑞-Zeta Functions and Associated Series and Integrals (1st ed.). Elsevier.
- Wang, W., & Xu, C. (2021). Alternating multiple zeta values, and explicit formulas of some Euler–Apéry-type series. European Journal of Combinatorics, 93, Article 103283.
Manuscript history
- Received: 30 June 2022
- Revised: 9 January 2023
- Accepted: 23 February 2023
- Online First: 27 February 2023
Copyright information
![]() Ⓒ 2023 by the Authors.
Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Haukkanen, P. (2024). Quotients of sequences under the binomial convolution. Notes on Number Theory and Discrete Mathematics, 30(4), 681-690.
Cite this paper
Batır, N., & Sofo, A. (2023). Sums involving the binomial coefficients, Bernoulli numbers of the second kind and harmonic numbers. Notes on Number Theory and Discrete Mathematics, 29(1), 78-97, DOI: 10.7546/nntdm.2023.29.1.78-97.


