Objects generated by an arbitrary natural number. Part 3: Standard modal-topological aspect

Krassimir Atanassov
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 1, Pages 171–180
DOI: 10.7546/nntdm.2023.29.1.171-180
Full paper (PDF, 262 Kb)

Details

Authors and affiliations

Krassimir Atanassov
¹ Department of Bioinformatics and Mathematical Modelling,
Institute of Biophysics and Biomedical Engineering, Bulgarian Academy of Sciences
Acad. G. Bonchev Str., Bl. 105, Sofia-1113, Bulgaria
² Intelligent Systems Laboratory
Prof. Asen Zlatarov University, Bourgas-8000, Bulgaria

Abstract

The set generated by an arbitrary natural number , was defined in [3]. There, and in [4], some arithmetic functions and arithmetic operators of a modal type are defined over the elements of . Here, over the elements of arithmetic operators of a topological type are defined and some of their basic properties are studied. Perspectives for future research are discussed.

Keywords

• Arithmetic function
• Modal operator
• Natural number
• Set
• Topological operator

2020 Mathematics Subject Classification

• 11A25

References

1. Atanassov, K. (1985). Short proof of a hypothesis of A. Mullin. Bulletin of Number Theory and Related Topics, IX(2), 9–11.
2. Atanassov, K. (1999). Intuitionistic Fuzzy Sets: Theory and Applications. Springer, Heidelberg.
3. Atanassov, K. (2020). Objects generated by an arbitrary natural number. Notes on Number Theory and Discrete Mathematics, 26(4), 57–62.
4. Atanassov, K. (2022). Objects generated by an arbitrary natural number. Part 2: Modal aspect. Notes on Number Theory and Discrete Mathematics, 28(3), 558–563.
5. Atanassov, K. (2022). Intuitionistic Fuzzy Modal Topological Structure. Mathematics, 10, Article 3313.
6. Atanassov, K. (2022). On the Intuitionistic Fuzzy Modal Feeble Topological Structures. Notes on Intuitionistic Fuzzy Sets, 28(3), 211–222.
7. Blackburn, P., van Bentham, J., & Wolter, F. (2006). Modal Logic. North Holland, Amsterdam.
8. Bourbaki, N. (1960). Éléments De Mathématique, Livre III: Topologie Générale (3rd ed.). Chapitre 1: Structures Topologiques, Chapitre 2: Structures Uniformes. Herman, Paris.
9. Feys, R. (1965). Modal Logics. Gauthier, Paris.
10. Fitting, M., & Mendelsohn, R. (1998). First Order Modal Logic. Kluwer, Dordrecht.
11. Kuratowski, K. (1966). Topology, Vol. 1. Academic Press, New York.
12. Sándor, J., & Crstici, B. (2005). Handbook of Number Theory. II. Springer Verlag, Berlin.

Manuscript history

• Received: 4 October 2022
• Revised: 11 March 2023
• Accepted: 21 March 2023
• Online First: 27 March 2023
• Correction Notice: 23 August 2023
  Per Author’s request made on 23 August 2023, the following correction is made on page 173, line -11 of the Online First (electronic) version:
  Old: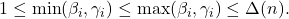         
  New: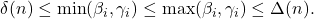

Copyright information

Ⓒ 2023 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).