Thorranin Thansri, Teerapat Srichan and Pinthira Tangsupphathawat
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 1, Pages 17–23
DOI: 10.7546/nntdm.2023.29.1.17-23
Full paper (PDF, 190 Kb)
Details
Authors and affiliations
Thorranin Thansri ![]()
![]()
Department of Mathematics, Faculty of Science
Kasetsart University, Bangkok 10900, Thailand
Teerapat Srichan ![]()
![]()
Department of Mathematics, Faculty of Science
Kasetsart University, Bangkok 10900, Thailand
Pinthira Tangsupphathawat ![]()
![]()
Department of Mathematics, Faculty of Science and Technology
Phranakorn Rajabhat University, Bangkok 10220, Thailand
Abstract
Let ![]() and
and ![]() denote relatively prime positive integers. In this article, we derive the asymptotic formula for the summation
denote relatively prime positive integers. In this article, we derive the asymptotic formula for the summation
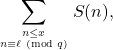
where ![]() denotes the number of non-isomorphic finite semisimple rings with
denotes the number of non-isomorphic finite semisimple rings with ![]() elements.
elements.
Keywords
- Abelian group
- Arithmetical progression
- Asymptotic mean value
- Counting function
- Semisimple group
2020 Mathematics Subject Classification
- 11N45
- 11N37
References
- Calderón, C. (2003). Asymptotic estimates on finite abelian groups. Publications de l’Institut Mathématique, 74(88), 57–70.
- Calderón, C., & Zárate, M. J. (1992). The number of semisimple rings of order at most x. Extracta Mathematicae, 7(2-3), 144–147.
- Connell, I. G. (1964). A number theory problem concerning finite groups and rings. Canadian Mathematical Bulletin, 7, 23–34.
- Duttlinger, J. (1974). Eine Bemerkung zu einer asymptotischen Formel von Herrn Knopfmacher. Journal für die reine und angewandte Mathematik, 266, 104–106.
- Erdős, P., & Szekeres, G. (1934). Über die Anzahl der Abelschen Gruppen gegebener Ordnung und über ein verwandtes zahlentheoretisches Problem. Acta Scientiarum Mathematicarum (Szeged), 7, 95–102.
- Ivic, A. (1985). ´ The Theory of the Riemann Zeta Function. Wiley, New York.
- Kendall, D. G., & Rankin, R. A. (1947). On the number of abelian groups of a given order. The Quarterly Journal of Mathematics, 18(1), 197–208.
- Knopfmacher, J. (1972). Arithmetical properties of finite rings and algebras, and analytic number theory. I. Journal für die reine und angewandte Mathematik, 252, 16–43.
- Kolesnik, G. (1981). On the number of Abelian groups of a given order. Journal für die reine und angewandte Mathematik, 329, 164–175.
- Liu, H. Q. (1991). On the number of abelian groups of a given order. Acta Arithmetica, 59, 261–277.
- Richert, H.-E. (1952). Über die Anzahl Abelscher Gruppen gegebener Ordnung. I.
Mathematische Zeitschrift, 56, 21–32. - Richert, H.-E. (1953). Über die Anzahl Abelscher Gruppen gegebener Ordnung. II. Mathematische Zeitschrift, 58(1), 71–84 .
- Sargos, P., & Wu, J. (2000). Multiple exponential sums with monomials and their
applications in number theory. Acta Mathematica Hungarica, 87(4), 333–354. - Schmidt, P. G. (1968). Zur Anzahl Abelscher Gruppen gegebener Ordnung. Journal für die reine und angewandte Mathematik, 229, 34–42.
- Schmidt, P. G. (1968). Zur Anzahl Abelscher Gruppen gegebener Ordnung II. Acta Arithmetica, 13, 405–417.
- Schwarz, W. (1966). Über die Anzahl Abelscher Gruppen gegebener Ordnung I.
Mathematische Zeitschrift, 92, 314–320.
Manuscript history
- Received: 20 September 2022
- Revised: 26 November 2022
- Accepted: 31 January 2023
- Online First: 6 February 2023
Copyright information
![]() Ⓒ 2023 by the Authors.
Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Thansri, T., Srichan, T., & Tangsupphathawat, P. (2023). On distribution of the number of semisimple rings of order at most x in an arithmetic progression. Notes on Number Theory and Discrete Mathematics, 29(1), 17-23, DOI: 10.7546/nntdm.2023.29.1.17-23.


