On a generalization of Eulerian numbers

Claudio Pita-Ruiz
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 24, 2018, Number 1, Pages 16–42
DOI: 10.7546/nntdm.2018.24.1.16-42
Full paper (PDF, 261 Kb)

Details

Authors and affiliations

Claudio Pita-Ruiz
Facultad de Ingenierıa, Universidad Panamericana
Augusto Rodin 498, Mexico, Ciudad de Mexico, 03920, Mexico

Abstract

We consider the sequence 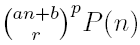, product of the rp-th degree n-polynomial 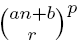, where a, b ∈ ℂ, a ≠ 0, r, p ∈ ℕ, and the -th degree n-polynomial , where α_s, β_s ∈ ℂ, r_s, p_s ∈ ℕ, s = 2, …, l. In the expansion of the polynomial 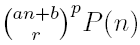in terms of the binomials , , the resulting coefficients are the generalized Eulerian numbers we consider in this work (the case P(n) = 1, a = 1, b = 0, r = 1 corresponds to the standard Eulerian numbers). We obtain results on symmetries, recurrences, row sums, and alternating row sums, that generalize the corresponding well-known results for the standard Eulerian numbers. The main tool we use to obtain our results throughout the work, is the Z-transform of sequences.

Keywords

• Generalized Eulerian numbers

2010 Mathematics Subject Classification

• 11B83

References

1. Carlitz, L. (1952) Note on a Paper of Shanks, Amer. Math. Monthly, 59, 4, 239–241.
2. Carlitz, L. (1978) A Note on q-Eulerian Numbers, J. Combin. Theory Ser. A, 25, 90–94.
3. Carlitz, L. (1959) Eulerian numbers and polynomials, Math. Mag., 32, 247–260.
4. Carlitz, L. (1954) q-Bernoulli and Eulerian numbers, Trans. Amer. Math. Soc., 76, 332–350.
5. Carlitz, L. (1975) A combinatorial property of q-Eulerian numbers, Amer. Math. Monthly, 82, 51–54.
6. Carlitz, L. (1960) Eulerian numbers and polynomials of higher order, Duke Math. J., 27, 401–423.
7. Carlitz, L. (1964) Extended Bernoulli and Eulerian numbers, Duke Math. J., 31, 667–689.
8. Carlitz, L., & Riordan, J. (1953) Congruences for Eulerian Numbers, Duke Math. J., 20, 339–343.
9. Dilcher, K. Bernoulli and Euler Polynomials, Digital Library of Mathematical Functions, Chapter 24. Available at: http://dlmf.nist.gov/24.
10. Euler, L. (1755) Institutiones Calculi Differentialis, Academiae Imperialis Scientiarum Petropolitanae.
11. Foata, D. (2010) Eulerian Polynomials: from Euler’s Time to the Present, in “The Legacy of Alladi Ramakrishnan in the Mathematical Sciences”, Springer, 253–273.
12. Foata, D., & Schutzenberger, M. P. (1970) Theorie geometrique des polynomes Euleriens, Lecture Notes in Mathematics, Vol. 138, Springer.
13. Gould, H. W. (1972) Combinatorial Identities, Morgantown, W. Va.
14. Graf, U. (2004) Applied Laplace Transforms and z-Transforms for Scientists and Engineers: A Computational Approach using a Mathematica Package, Birkh¨auser.
15. Hsu, L. C., & Shiue, P. J. S. (1999) On certain summation problems and generalizations of Eulerian polynomials and numbers, Discrete Math., 204, 237–247.
16. Koutras, M. V. (1994) Eulerian Numbers Associated with Sequences of Polynomials, Fibonacci Quart., 32, 44–57.
17. Lehmer, D. H. (1982) Generalized Eulerian Numbers, J. Combin. Theory Ser. A, 32, 195–215.
18. Lin, Z. (2013) On some generalized q-Eulerian polynomials, DMTCS Proc. AS., 439–450.
19. Petersen, T. K. (2015) Eulerian Numbers, Birkhauser.
20. Savage, C. D., & Viswanathan, G., The 1/k-Eulerian Polynomials, Available online at: http://www4.ncsu.edu/~savage/PAPERS/The_1_over_k_Eulerian_Polynomials.pdf.
21. Shanks, E. B. (1951) Iterated Sums of Powers of the Binomial Coefficients, Amer. Math. Monthly, 58, 404–407.
22. Stanley, R. P. (1997) Enumerative Combinatorics, Vol. 1, Cambridge Studies in Advanced Mathematics, 49, Cambridge University Press.
23. Vilch, R. (1987) Z Transform. Theory and Applications, D. Reidel Publishing Company.
24. Worpitzky, J. (1883) Studien ¨uber die Bernoullischen und Eulerschen Zahlen, J. Reine Angew. Math., 94, 203–232.
25. Xiong, T., Tsao, H. P., & Hall, J. I. (2013) General Eulerian Numbers and Eulerian Polynomials, Journal of Mathematics, Vol. 2013, ID 629132.