Laurențiu Panaitopol
Notes on Number Theory and Discrete Mathematics
ISSN 1310–5132
Volume 8, 2002, Number 4, Pages 145–148
Full paper (PDF, 128 Kb)
Details
Authors and affiliations
Laurențiu Panaitopol
University of Bucharest, Faculty of Mathematics
14 Academiei St., RO-70109 Bucharest, Romania
Abstract
For ![]() , let
, let ![]() be the number of prime numbers not exceeding
be the number of prime numbers not exceeding ![]() . One shows that, for
. One shows that, for ![]() , there exists at least one prime number between
, there exists at least one prime number between ![]() and
and ![]() , thus obtaining a result that is sharper than the one postulated by Bertrand.
, thus obtaining a result that is sharper than the one postulated by Bertrand.
Keywords
- Distribution of prime numbers
- Inequalities
- Bertrand’s postulate
AMS Classification
- 11A35
- 11N05
References
- Bertrand .J., Memoire sur le nombre de valeurs que pent prendre une function quand on y permute les lettres qu’elle renferme. J. L’Ecole Royale Polytechn. 18 (1845), 123-140.
- Chebyshev P.L., Memoire sur le nombres premiers. J. Math. Pures Appl. 17 (1852), 366-390.
- Costa Pereira N., Elementary estimate for the Chebyshev function
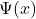 and the Mobius function
and the Mobius function 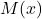 . Acta Arith. 52 (1989), 307-337.
. Acta Arith. 52 (1989), 307-337. - Dusart P., Inegalites explicites pour
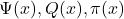 et les nombres premiers. C. R. Math. Acad. Sci. Soc. R. Can. 2 (1999), 53-59.
et les nombres premiers. C. R. Math. Acad. Sci. Soc. R. Can. 2 (1999), 53-59. - Mitrinovic D.S., Sándor J., Crstici B., Handbook of Number Theory. Kluwer Academic Publishers, Dordrecht-Boston-London, 1996.
- Nagura J., On the interval containing at least one prime number. Proc. Japan. Acad. 28 (1952), 177-181.
- Panaitopol L., A special case of the Hardy–Littlewood conjecture. Math. Reports (to appear).
- Rohrbach H., Weis J., Zum finiten Fall des Bertrandschen Postulats. J. reine angew. Math. 214/215 (1964), 432-440.
- Rosser J.B., Schoenfeld L., Approximate formulas for functions of prime numbers. Illinois J. Math. 6 (1962), 64-94.
Related papers
Cite this paper
Panaitopol, L. (2002). Intervals containing prime numbers. Notes on Number Theory and Discrete Mathematics, 8(4), 145-148.


