A partial recurrence Fibonacci link

Anthony G. Shannon, Hakan Akkuş, Yeşim Aküzüm, Ömür Deveci and Engin Özkan
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 3, Pages 530–537
DOI: 10.7546/nntdm.2024.30.3.530-537
Full paper (PDF, 770 Kb)

Details

Authors and affiliations

Anthony G. Shannon
Warrane College, the University of New South Wales
Kensington 2033, Australia

Hakan Akkuş
Department of Mathematics, Graduate School of Natural and Applied Sciences,
Erzincan Binali Yıldırım University
Yalnızbağ Campus, 24100, Erzincan, Türkiye

Yeşim Aküzüm
Department of Mathematics, Faculty of Sciences and Letters, Kafkas University
36100 Kars, Türkiye

Ömür Deveci
Department of Mathematics, Faculty of Sciences and Letters, Kafkas University
36100 Kars, Türkiye

Engin Özkan
Department of Mathematics, Faculty of Sciences, Marmara University
İstanbul, Türkiye

Abstract

The purpose of this note is to develop a conjecture for a Fibonacci number generating function in terms of the elements of a second-order two parameter partial recurrence relation which arose in an operations research problem on Poisson distributed lead time in inventory control.

Keywords

• Fibonacci numbers
• Lucas numbers
• Operations research
• Partial recurrence relations

2020 Mathematics Subject Classification

• 11B30
• 11K31

References

1. Akkuş, H., Deveci, Ö., Özkan, E., & Shannon, A. G. (2024). Discatenated and lacunary recurrences. Notes on Number Theory and Discrete Mathematics, 30(1), 8–19.
2. Brousseau, A. (1967). Summation of 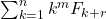finite difference approach. The Fibonacci Quarterly, 5(1), 91–98.
3. Çelik, S., Durukan, İ., & Özkan, E. (2021). New recurrences on Pell numbers, Pell–Lucas numbers, Jacobsthal numbers, and Jacobsthal–Lucas numbers. Chaos, Solitons and Fractals, 150(3), Article ID 111173.
4. Hadley, G., & Whitin, T. M. (1963). Analysis of Inventory Systems. NJ: Prentice-Hall.
5. Kumari, M., Prasad, K., & Frontczak, R. (2023). On the k-Fibonacci and k-Lucas spinors. Notes on Number Theory and Discrete Mathematics, 29(2), 322–335.
6. Ledin, G. (1967). On a certain kind of Fibonacci sums. The Fibonacci Quarterly, 5(1), 1, 45.
7. Ollerton, R. L., & Shannon, A. G. (2020). A note on Brousseau’s summation problem. The Fibonacci Quarterly, 58(5), 190–199.
8. Shannon, A. G., & Ollerton, R. L. (2021). A note on Ledin’s summation problem. The Fibonacci Quarterly, 59(1), 47–56.
9. Sloane, N. J. A. (2024). OEIS Foundation Inc., The On-Line Encyclopedia of Integer Sequences. Available online at: http://oeis.org.
10. Stanton, H. G. (1983). A marginal distribution of lead time demand based on a discrete lead time distribution. New Zealand Journal of Operational Research, 11(1), 31–39.
11. Zhang, C., Khan, W. A., & Kızılateş, C. (2023). On (p, q)-Fibonacci and (p, q)-Lucas polynomials associated with Changhee numbers and their properties. Symmetry, 15(4), Article ID 851.

Manuscript history

• Received: 7 May 2023
• Revised: 19 September 2024
• Accepted: 29 September 2024
• Online First: 30 September 2024

Copyright information

Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).