Kunle Adegoke, Robert Frontczak and Taras Goy
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 2, Pages 319–334
DOI: 10.7546/nntdm.2024.30.2.319-334
Full paper (PDF, 280 Kb)
Details
Authors and affiliations
Kunle Adegoke ![]()
![]()
Department of Physics and Engineering Physics, Obafemi Awolowo University
220005 Ile-Ife, Nigeria
Robert Frontczak ![]()
![]()
Independent Researcher
Reutlingen, Germany
Taras Goy ![]()
![]()
Faculty of Mathematics and Computer Science, Vasyl Stefanyk Precarpathian National University
76018 Ivano-Frankivsk, Ukraine
Abstract
Using a simple transformation, we obtain much simpler forms for some series involving binomial coefficients ![]() derived by Necdet Batır. New evaluations are given and connections with Fibonacci numbers and the golden ratio are established. Finally we derive some Fibonacci and Lucas series involving the reciprocals of
derived by Necdet Batır. New evaluations are given and connections with Fibonacci numbers and the golden ratio are established. Finally we derive some Fibonacci and Lucas series involving the reciprocals of ![]() .
.
Keywords
- Digital sums
- Asymptotic
- Error term
2020 Mathematics Subject Classification
- 11A25
- 11A63
- 11N37
References
- Batır, N. (2003). On the series
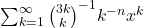 . Proceedings of the Indian Academy of Sciences: Mathematical Sciences, 115, 371–381.
. Proceedings of the Indian Academy of Sciences: Mathematical Sciences, 115, 371–381. - Borwein, J. M., & Girgensohn, R. (2005). Evaluations of binomial series. Aequationes Mathematicae, 70, 25–36.
- Chu, W. (2022). Gosper-type sums with reciprocals of binomial coefficients of the form
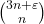 . Journal of Difference Equations and Applications, 28, 1381–1404.
. Journal of Difference Equations and Applications, 28, 1381–1404. - D’Aurizio, J., & Di Trani, S. (2018). Surprising identities for the hypergeometric
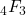 function. Bolletino dell Unione Matematica Italiana, 11, 403–409.
function. Bolletino dell Unione Matematica Italiana, 11, 403–409. - Koshy, T. (2017). Fibonacci and Lucas Numbers with Applications. Wiley, New York.
- Lehmer, D. H. (1985). Interesting series involving the central binomial coefficient. The American Mathematical Monthly, 92, 449–457.
- Vajda, S. (2008). Fibonacci & Lucas numbers, and the Golden Section: Theory and Applications. Dover, New York.
Manuscript history
- Received: 19 February 2024
- Revised: 13 May 2024
- Accepted: 13 May 2024
- Online First: 20 May 2024
Copyright information
![]() Ⓒ 2024 by the Authors.
Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Akerele, S. O., & Salami, O. E. (2025). Series associated with harmonic numbers, Fibonacci numbers and central binomial coefficients
. Notes on Number Theory and Discrete Mathematics, 31(1), 82-90.
Cite this paper
Adegoke, K., Frontczak, R., & Goy, T. (2024). On some series involving the binomial coefficients ![]() . Notes on Number Theory and Discrete Mathematics, 30(2), 319-334, DOI: 10.7546/nntdm.2024.30.2.319-334.
. Notes on Number Theory and Discrete Mathematics, 30(2), 319-334, DOI: 10.7546/nntdm.2024.30.2.319-334.


