József Sándor
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 18, 2014, Number 1, Pages 1–5
Full paper (PDF, 165 Kb)
Details
Authors and affiliations
József Sándor ![]()
![]()
Babeș-Bolyai University, Department of Mathematics
Str. Kogălniceanu nr. 1, 400084 Cluj-Napoca, Romania
Abstract
We will consider various limits and inequalities connected with the n-th prime number.
Keywords
- Arithmetic functions
- Primes
- Estimates
AMS Classification
- 11A25
- 11N37
References
- Alzer, H., J. Sándor, On a binomial coefficient and a product of prime numbers, Appl. Anal. Discr. Math. , Vol. 5, 2011, 87–92
- Gupta, H., S. P. Khare, On
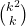 and the product of the first k primes, Univ. Beograd Publ. Elektr. Fak. Ser. Mat. Fiz., Vol. 577–598, 1977, 25–29.
and the product of the first k primes, Univ. Beograd Publ. Elektr. Fak. Ser. Mat. Fiz., Vol. 577–598, 1977, 25–29. - Goldston, D. A., J. Pintz, C. Y. Yildirim, Primes in tuples I, Annals of Math. , Vol. 170, 2009, 819–862
- Mitrinović, D. S., J. Sándor, B. Crstici. Handbook of number theory, Kluwer Acad. Publ., 1996
- Panaitopol, L. An inequality concerning the prime numbers. Notes on Number Theory and Discrete Mathematics, Vol. 5, 1999, No. 2, 52–54.
- Panaitopol, L. An inequality involving prime numbers, Univ. Beograd Publ. Elektrotehn. Fak. Ser. Mat., Vol. 11, 2000, 33–35.
- Rosser, J. B., L. Schoenfeld, Approximate formulas for some functions of prime numbers, Illinois J. Math. , Vol. 6, 1962, 64–94.
- Sándor, J., A. Verroken, On a limit involving the product of prime numbers. Notes on Number Theory and Discrete Mathematics, , Vol. 17, 2011, No. 2, 1–3.
- Sándor, J. Selected chapters of geometry, analysis and number theory, classical topics in new perspectives, Lambert Acad. Publ., 2008
- Westzynthius, E. Uber die Verteilung der Zahlen die zu den ersten Primzahlen teilerfremd sind, Comm. Phys. Math. Soc. Fenn. , Helsingfors, Vol. 5, 1931, 1–37
Related papers
Cite this paper
Sándor, J. (2012). On certain bounds and limits for prime numbers. Notes on Number Theory and Discrete Mathematics, 18(1), 1-5.


