Nabil Tahmi and Abdallah Derbal
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 4, Pages 603–616
DOI: 10.7546/nntdm.2022.28.4.603-616
Full paper (PDF, 216 Kb)
Details
Authors and affiliations
Nabil Tahmi ![]()
Department of Mathematics, ENS of Laghouat and EDPNLHM Laboratory,
ENS of Kouba, Algiers, Algeria
Abdallah Derbal ![]()
![]()
Department of Mathematics, EDPNLHM Laboratory,
ENS of Kouba, Algiers, Algeria
Abstract
Let ![]() be an arithmetic function of
be an arithmetic function of ![]() variables, where
variables, where ![]() . We study multiple Dirichlet series defined by
. We study multiple Dirichlet series defined by
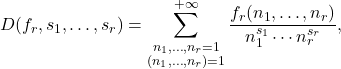
where ![]() and
and ![]() is a completely multiplicative or a specially multiplicative arithmetic function of a single variable. We obtain formulas for these series expressed by infinite products over the primes. We also consider the cases of certain particular completely multiplicative and specially multiplicative functions.
is a completely multiplicative or a specially multiplicative arithmetic function of a single variable. We obtain formulas for these series expressed by infinite products over the primes. We also consider the cases of certain particular completely multiplicative and specially multiplicative functions.
Keywords
- Completely multiplicative function
- Specially multiplicative function
- Multiple Dirichlet series
- Eulerian product
- Riemann zeta function
- Dirichlet L-function
2020 Mathematics Subject Classification
- 11M32, 11M06, 11A25
References
- Apostol, T. M. (1976). Introduction to Analytic Number Theory, Springer-Verlag, New York.
- McCarthy, P. J. (1986). Introduction to Arithmetical Functions. Springer.
- Nowak, W. G., & Tóth, L. (2014). On the average number of subgroups of the group Zm × Zn. International Journal of Number Theory, 10(2), 363–374.
- Tóth, L. (2010). A survey of gcd-sum functions. Journal of Integer Sequences, 13, 2–3. (Article 10.8.1).
- Tóth, L. (2011). Menon’s identity and arithmetical sums representing functions of several variables. Rendiconti del Seminario Matematico Universita e Politecnico di Torino, 69, 97–110.
- Tóth, L. (2013). Two generalizations of the Busche–Ramanujan identities. International Journal of Number Theory, 9, 1301–1311.
- Tóth, L. (2014). Multiplicative Arithmetic Functions of Several Variables: A Survey. In: Rassias, Th. M., & Pardalos, P. (Eds.) Mathematics Without Boundaries, Surveys in Pure Mathematics. Springer, New York, pp. 483–514.
- Tóth, L., & Zhai, W. (2010). On multivariable averages of divisor functions. Journal of Number Theory, 192(1), 251–269.
Manuscript history
- Received: 22 February 2022
- Revised: 23 September 2022
- Accepted: 12 October 2022
- Online First: 14 October 2022
Related papers
Cite this paper
Tahmi, N., & Derbal, A. (2022). Some multiple Dirichlet series of completely multiplicative arithmetic functions. Notes on Number Theory and Discrete Mathematics, 28(4), 603-616, DOI: 10.7546/nntdm.2022.28.4.603-616.


