Yücel Türker Ulutaş and Derya Toy
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 2, Pages 252–260
DOI: 10.7546/nntdm.2022.28.2.252-260
Full paper (PDF, 146 Kb)
Details
Authors and affiliations
Yücel Türker Ulutaş ![]()
Department of Mathematics, University of Kocaeli
Kocaeli, Turkey
Derya Toy ![]()
Institute of Science and Technology, University of Kocaeli
Kocaeli, Turkey
Abstract
In this study, we take the generalized Fibonacci sequence ![]() as
as ![]() and
and ![]() for
for ![]() , where
, where ![]() is a non-zero integer. Based on Halton’s paper in [4], we derive three interrelated functions involving the terms of generalized Fibonacci sequence
is a non-zero integer. Based on Halton’s paper in [4], we derive three interrelated functions involving the terms of generalized Fibonacci sequence ![]() . Using these three functions we introduce a simple approach to obtain a lot of identities, binomial sums and alternate binomial sums involving the terms of generalized Fibonacci sequence
. Using these three functions we introduce a simple approach to obtain a lot of identities, binomial sums and alternate binomial sums involving the terms of generalized Fibonacci sequence ![]() .
.
Keywords
- Generalized Fibonacci numbers
- Sums of generalized Fibonacci numbers
- Binomial sums
2020 Mathematics Subject Classification
- 11B37
- 11B39
- 11B65
References
- Adegoke, K. (2018). Fibonacci and Lucas identities the golden way. arXiv. https://doi.org/10.48550/arXiv.1810.12115.
- Bicknell, M. (1975). A primer on the Pell sequences and related sequences. The Fibonacci Quarterly, 13(4), 345–349.
- Filipponi, P., & Horadam, A. F. (1993). Second derivative sequences of the Fibonacci and Lucas polynomials. The Fibonacci Quarterly, 31(3), 194–204.
- Halton, J. H. (1965). On a general Fibonacci identity. The Fibonacci Quarterly, 3(1), 31–43.
- Horadam, A. F. (1965). Basic properties of a certain generalized sequence of number. The Fibonacci Quarterly, 3(3), 161–176.
- Horadam, A. F. (1965). Generating functions for powers of a certain generalized sequence of numbers. Duke Mathematical Journal, 32, 437–446.
- Kılıç, E., Ömür, N., & Türker Ulutaş, Y., (2009). Matrix representation of the second order recurrence
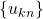 . Ars Combinotaria, 93, 181–190.
. Ars Combinotaria, 93, 181–190. - Kılıç, E., Ömür, N., & Türker Ulutaş, Y. (2011). Binomial sums whose coefficients are products of terms of binary sequences. Utilitas Mathematica, 84, 45–52.
- Kılıç, E., Türker Ulutaş, Y., & Ömür, N. (2012). Formulas for weighted binomial sums with the powers of terms of binary recurrences. Miskolc Mathematical Notes, 13(1), 53–65.
- Komatsu, T., & Cook, C. K. (2016). Some identities for sequences of binomial sums of generalized Fibonacci numbers. The Fibonacci Quarterly, 54(2), 105–111.
- Koshy, T. (2018). Fibonacci and Lucas Numbers with Applications. A Wiley-Interscience Publication, New York.
- Layman, J. W. (1977). Certain general binomial-Fibonacci sums. The Fibonacci Quarterly, 15(4), 362–366.
- Seibert, J., & Trojovsky, P. (2006). On sums of certain products of Lucas numbers. The Fibonacci Quarterly, 44(2), 172–180.
- Soykan, Y. (2020). Generalized Fibonacci numbers: Sum formulas. Journal of Advances in Mathematics and Computer Science, 35(1), 89–104.
Manuscript history
- Received: 4 June 2021
- Revised: 28 April 2022
- Accepted: 5 May 2022
- Online First: 6 May 2022
Related papers
Cite this paper
Türker Ulutaş, Y., & Toy, D. (2022). Some equalities and binomial sums about the generalized Fibonacci number un. Notes on Number Theory and Discrete Mathematics, 28(2), 252-260, DOI: 10.7546/nntdm.2022.28.2.252-260.


