On a translated sum over primitive sequences related to a conjecture of Erdős

Nadir Rezzoug, Ilias Laib and Guenda Kenza
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367-8275
Volume 26, 2020, Number 4, Pages 68–73
DOI: 10.7546/nntdm.2020.26.4.68-73
Full paper (PDF, 156 Kb)

Details

Authors and affiliations

Nadir Rezzoug
Laboratory of Analysis and Control of Partial Differential Equations
Faculty of Exact Sciences, Djillali Liabes University
Sidi Bel Abbes, Algeria

Ilias Laib
ENSTP, Garidi Kouba, 16051, Algiers, Algeria
and Laboratory of Equations with Partial Non-Linear Derivatives
ENS Vieux Kouba, Algiers, Algeria

Guenda Kenza
Faculty of Mathematics, University of Sciences and Technology Houari Boumédiène,
Algiers, Algeria

Abstract

For x large enough, there exists a primitive sequence \mathcal{A}, such that

    \begin{equation*} \sum\limits_{a\in \mathcal{A}}\frac{1}{a(\log a+x)}\gg \sum\limits_{p\in \mathcal{P}}\frac{1}{p(\log p+x)}\text{,} \end{equation*}

where \mathcal{P} denotes the set of prime numbers.

Keywords

  • Primitive sequences
  • Erdős conjecture
  • Prime numbers

2010 Mathematics Subject Classification

  • 11Bxx

References

  1. Dusart., P. (1998). Autour de la fonction qui compte le nombre de nombres premiers, thèse de doctorat, université de Limoges, 17-1998.
  2. Erdős, P. (1935). Note on sequences of integers no one of which is divisible by any other, J.Lond. Math. Soc, 10, 126–128.
  3. Erdős, P., & Zhang, Z. (1993). Upper bound of 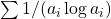\sum 1/(a_{i}\log a_{i}) for primitive sequences, Math. Soc, 117, 891–895.
  4. Farhi, B. (2017). Results and conjectures related to a conjecture of Erdős concerning primitive sequences, arXiv: 1709.08708v2 [math.NT] 25 Sep 2017.
  5. Laib, I., Derbal, A. & Mechik, R. (2019). Somme translatée sur des suites primitives et la conjecture d’Erdős. C. R. Acad. Sci. Paris, Ser. I, 357, 413–417.
  6. Massias, J.-P., & Robin, G. (1996). Bornes effectives pour certaines fonctions concernant les nombres premiers, J. Theori. Nombres Bordeaux, 8, 215–242.
  7. Robbins, H. (1955). A remark on Stirling’s formula, Amer. Math. Monthly, 62, 26–29.
  8. Rosser, J. B., & Schoenfeld, L. (1962). Approximates formulas for some functions of prime numbers, Illinois Journal Math, 6, 64–94.

Related papers

Cite this paper

Rezzoug, N., Laib, I. & Kenza, G. (2020). On a translated sum over primitive sequences related to a conjecture of Erdős. Notes on Number Theory and Discrete Mathematics, 26 (4), 68-73, DOI: 10.7546/nntdm.2020.26.4.68-73.

Comments are closed.