Fibonacci primes of special forms

Diana Savin
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 20, 2014, Number 2, Pages 10–19
Full paper (PDF, 202 Kb)

Details

Authors and affiliations

Diana Savin
Ovidius University of Constanta
Faculty of Mathematics and Computers Science
Bd. Mamaia no. 124, Constanta, 900527, Romania

Abstract

A study of Fibonacci primes of the form x2 + ry2 (where r = 1; r = prime or r = perfect power) is provided.

Keywords

  • Fibonacci numbers
  • Quadratic fields
  • Computational number theory
  • Algebraic number theory computations

AMS Classification

  • 11D25
  • 11S15
  • 11Y40
  • 11Y50

References

  1. Azizi, A., A. Mouhib, Sur le rang du 2-groupe de classes de 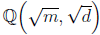\mathbb{Q}\left(\sqrt{m},\sqrt{d}\right) ou m = 2 ou un premier p ≡ 1 (mod 4). Transactions of the American Mathematical Society, Vol. 353, 2001, No. 7, 2741–2752.
  2. Ballot, C., F. Luca, On the equation x2 + dy2 = Fn, Acta Arithmetica, Vol. 172, 2007, No. 2, 145–155.
  3. Cox, D. Primes of the Form x2 + ny2: Fermat, Class Field Theory, and Complex Multiplication, A Wiley – Interscience Publication, New York, 1989.
  4. Kubota,T. Uber den bizyklischen biquadratischen Zahlkorper. Nagoya Math. Journal, Vol. 10, 1956, 65–85.
  5. Lehmer, E. On the Cubic Character of Quadratic Units. Journal of Number Theory, Vol. 5, 1973, 385–389.
  6. Lehmer, E. On the quartic character of quadratic units. J. Reine Angew. Math., Vol. 268/269, 1974, 294–301.
  7. Lemmermeyer, F. Reciprocity laws, from Euler to Eisenstein. Springer-Verlag, Heidelberg, 2000.
  8. Mouhib, A. On the parity of the class number of multiquadratic number fields. Journal of Number Theory, Vol. 129, 2009, 1205–1211.
  9. Savin, D., M. Stefanescu, Lectures of Arithmetic and Number theory, Edit. Matrix Rom, 2008 (in Romanian).
  10. Savin, D., Stefanescu, M. A necessary condition for certain Primes to be written in the form xq + ryq, Journal of Algebra and Its Applications, Vol. 10, 2011, No. 3, 435–443.
  11. Sun, Z. H. Congruences for Fibonacci numbers, http://www.hytc.cn/xsjl/szh
  12. Sun, Z. H., Z.W. Sun. Fibonacci numbers and Fermat’s last theorem. Acta Arithemtica, Vol. 60, 1992, 371–388.
  13. Sun, Z. H. Constructing x2 for primes p = ax2 + by2, Adv. in Appl. Math., Vol. 48, 2012, No. 1, 106–120.
  14. http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibmaths.html
  15. Magma algebra system, http://magma.maths.usyd.edu.au/magma/

Related papers

Cite this paper

Savin, D. (2014). Fibonacci primes of special forms. Notes on Number Theory and Discrete Mathematics, 20(2), 10-19.

Comments are closed.