s-th power of Fibonacci number of the form 2a + 3b + 5c

Nurettin Irmak and Bo He
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 4, Pages 102–109
DOI: 10.7546/nntdm.2019.25.4.102-109
Full paper (PDF, 235 Kb)

Details

Authors and affiliations

Nurettin Irmak
Department of Mathematics, Art and Science Faculty,
Niğde Ömer Halisdemir University, Turkey

Bo He
Institute of Mathematics, Aba Teachers University
Wenchuan, Sichuan, 623000 P. R. China

Abstract

In this paper, we solve the Diophantine equation F_{n}^{s}=2^{a}+3^{b}+5^{c}, where a,b,c and s are positive integers with 1\le \max \left\{a,b\right\} \leq c.

Keywords

  • Fibonacci numbers
  • Linear forms in logarithms
  • Reduction method
  • s-th power

2010 Mathematics Subject Classification

  • 11B39
  • 11J86

References

  1. Bertók, C., Hajdu, L., Pink, I. & Rábai, Z. (2017). Linear combinations of prime powers in binary recurrence sequences. Int. J. Number Theory, 13 (2), 261–271.
  2. Bugeaud, Y., Mignotte, M., & Siksek, S. (2006). Classical and modular approaches to exponential Diophantine equation. I. Fibonacci and Lucas perfect powers. Ann of Math, 163, 969–1018.
  3. Bravo, J. J., & Luca, F. (2012). Powers of two in generalized Fibonacci sequence.Rev Colombiana Math, 46, 67–79.
  4. Luca, F. & Szalay, L. (2007). Fibonacci numbers of the form 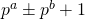p^a\pm p^b+ 1. The Fibonacci Quarterly, 45, 98–103.
  5. Marques, D. & Togbé, A. (2013). Fibonacci and Lucas numbers of the form 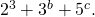2^3+ 3^b+ 5^c. Proc Japan Acad, 89, 47–50.
  6. Matveev, E. M. (2000). An explicit lower bound for a homogeneous linear form in logarithms of algebraic numbers. II, Izv Ross Akad Nauk Ser Mat, 64 (6), 125–180.
  7. Koshy, T. (2001). Fibonacci and Lucas Numbers with Applications, USA: Wiley.
  8. Luca, F. & Oyono, R. (2011). An exponential Diophantine equation related to powers of two consecutive Fibonacci numbers. Proc Japan Acad., 87 (A), 45–50.
  9. Shorey, T. N. & Stewart, C. L. (1987). Pure powers in recurrence sequences and some related Diophantine equations. J. Number Theory, 27 (3), 324–352.

Related papers

Cite this paper

Irmak, N., & He, B. (2019). s-th power of Fibonacci number of the form 2a + 3b + 5c. Notes on Number Theory and Discrete Mathematics, 25(4), 102-109, DOI: 10.7546/nntdm.2019.25.4.102-109.

Comments are closed.