Note on translated sum on primitive sequences

Ilias Laib
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 27, 2021, Number 3, Pages 39–43
DOI: 10.7546/nntdm.2021.27.3.39-43
Full paper (PDF, 189 Kb)

Details

Authors and affiliations

Ilias Laib
ENSTP, Garidi Kouba, 16051, Algiers,
and Laboratory of Equations with Partial Non-Linear Derivatives,
ENS Vieux Kouba, Algiers, Algeria

Abstract

In this note, we construct a new set \boldsymbol{S} of primitive sets such that for any real number x\geq 60 we get:

    \begin{equation*} \sum\limits_{a\in \mathcal{A}}\frac{1}{a(\log a+x)}>\sum\limits_{p\in \mathcal{P}}\frac{1}{p(\log p+x)},\text{ }\mathcal{A\in }{\boldsymbol{S}}, \end{equation*}

where \mathcal{P} denotes the set of prime numbers.

Keywords

  • Primitive sequences
  • Erdős’s conjecture
  • Prime numbers
  • Integer sequences

2020 Mathematics Subject Classification

  • 11B05
  • 11Y55
  • 11L20

References

  1. Clark, D. A. (1995). An upper bound of 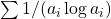\sum 1/(a_{i}\log a_{i}) for primitive sequences, Proceedings of the American Mathematical Society, 123, 363–365.
  2. Cohen, H. (1991). High precision computation of Hardy–Littlewood constants. Preprint. Available online at: http://www.math.u-bordeaux1.fr/~cohen/hardylw.dvi.
  3. Erdős, P. (1935). Note on sequences of integers no one of which is divisible by any other. Journal of the London Mathematical Society, 10(2), 126–128.
  4. Erdős, P. (1988). Seminar at the University of Limoges.
  5. Erdős, P., & Zhang, Z. (1993). Upper bound of 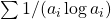\sum 1/(a_{i} \log a_{i}) for primitive sequences. Proceedings of the American Mathematical Society, 117(4), 891–895.
  6. Farhi, B. (2017). Results and conjectures related to a conjecture of Erdős concerning primitive sequences. Preprint. arXiv:1709.08708v2 [math.NT].
  7. Laib, I., Derbal, A., & Mechik, R. (2019). Somme translatee sur des suites primitives et la conjecture d’Erdős. Comptes Rendus Mathematique, 357(5), 413–417.
  8. Lichtman, J. D., & Pomerance, C. (2019). The Erdős conjecture for primitive sets. Proceedings of the American Mathematical Society Ser. B, 6, 1–14.
  9. Rezzoug, N., Laib, I., & Guenda, K. (2020). On a translated sum over primitive sequences related to a conjecture of Erdős. Notes on Number Theory and Discrete Mathematics, 26(4), 68–73.
  10. Rosser, J. B., & Schoenfeld, L. (1962). Approximates Formulas for Some Functions of Prime Numbers. Illinois Journal of Mathematics, 6, 64–94.
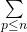
  11. Zhang, Z. (1991). On a conjecture of Erdős on the sum 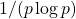\sum\limits_{p\leq n} 1/(p\log p). Journal of Number Theory, 39, 14–17.
  12. Zhang, Z. (1993). On a problem of Erdős concerning primitive sequences. Mathematics of Computation, 60(202), 827–834.

Related papers

  1. Rezzoug, N., Laib, I., & Guenda, K. (2020). On a translated sum over primitive sequences related to a conjecture of Erdős. Notes on Number Theory and Discrete Mathematics, 26(4), 68–73.

Cite this paper

Laib, I. (2021). Note on translated sum on primitive sequences. Notes on Number Theory and Discrete Mathematics, 27(3), 39-43, DOI: 10.7546/nntdm.2021.27.3.39-43.

Comments are closed.